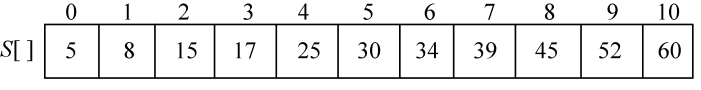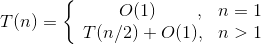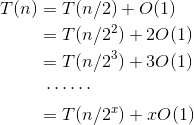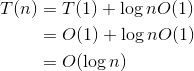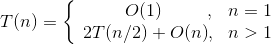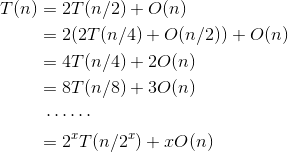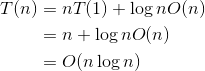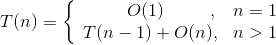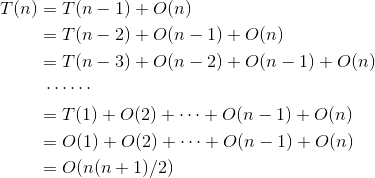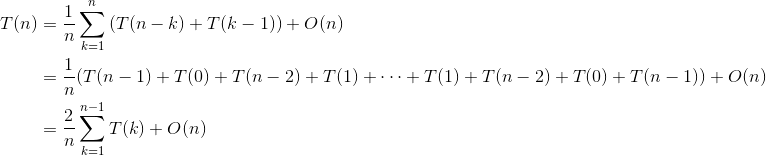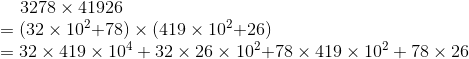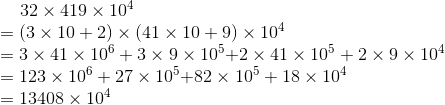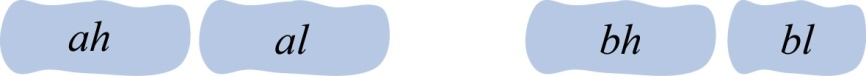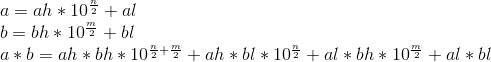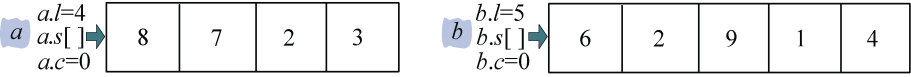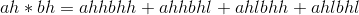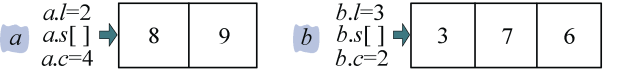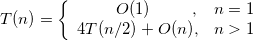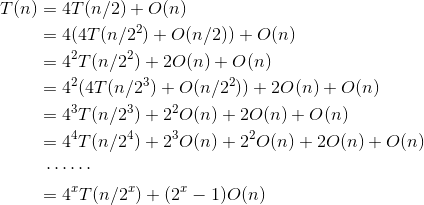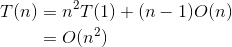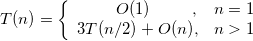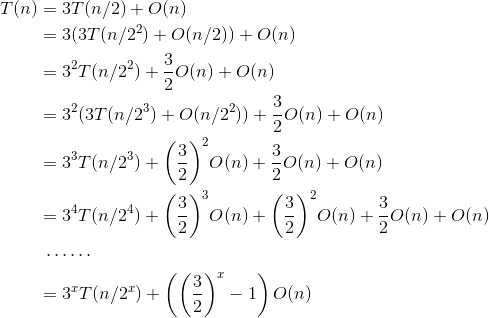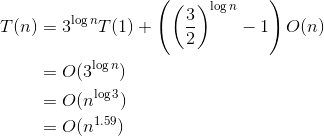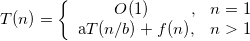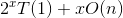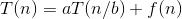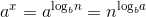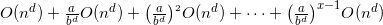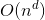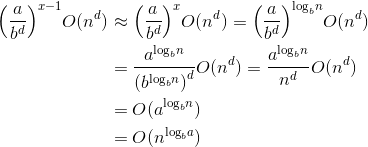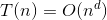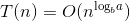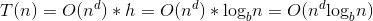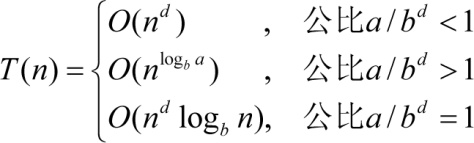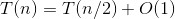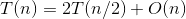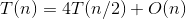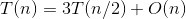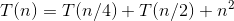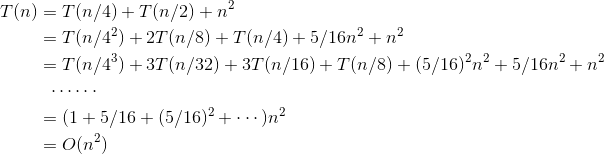《趣学算法》—第三章（分治法）

第三章　分治法

分而治之是一种很古老但很实用的策略，或者说战略，本意是将一个较大的力量打碎分成小的力量，这样每个小的力量都不足以对抗大的力量。在现实应用中，分而治之往往是将大片区域分成小块区域治理。战国时期，秦国破坏合纵连横即是一种分而治之的手段。

3.1　山高皇帝远

我们经常听到一句话：“山高皇帝远”，意思是山高路远，皇帝管不了。实际上无论山多高，皇帝有多远，都在朝庭的统治之下。皇帝一个人当然不可能管那么多的事情，那么怎么统治天下呢？分而治之。我们现在的制度也采用了分而治之的办法，国家分省、市、县、镇、村，层层管理，无论哪个偏远角落，都不是无组织的。

3.1.1　治众如治寡——分而治之

“凡治众如治寡，分数是也。”

——《孙子兵法》

“分数”的“分”是指分各层次的部分，“数”是每部分的人数编制，意为通过把部队分为各级组织，将帅就只需通过管理少数几个人来实现管理全军众多组织。这样，管理和指挥人数众多的大军，也如同管理和指挥人数少的部队一样容易。

在我们生活当中也有很多这样的例子，例如电视节目歌唱比赛，如果全国各地的歌手都来报名参赛，那估计要累坏评委了，而且一个一个比赛需要很长的时间，怎么办呢？全国分赛区海选，每个赛区的前几名再参加二次海选，最后选择比较优秀的选手参加电视节目比赛。这样既可以把最优秀的歌手呈现给观众，又节省了很多时间，因为全国各地分赛区的海选比赛是同步进行的，有点“并行”的意思。

在算法设计中，我们也引入分而治之的策略，称为分治算法，其本质就是将一个大规模的问题分解为若干个规模较小的相同子问题，分而治之。

3.1.2　天时地利人和——分治算法要素

“农夫朴力而寡能，则上不失天时，下不失地利，中得人和而百事不废。”

——《荀子•王霸篇》

也就是说，做成一件事，需要天时地利人和。那么在现实生活中，什么样的问题才能使用分治法解决呢？简单来说，需要满足以下3个条件。

（1）原问题可分解为若干个规模较小的相同子问题。

（2）子问题相互独立。

（3）子问题的解可以合并为原问题的解。

3.1.3　分治算法秘籍

分治法解题的一般步骤如下。

（1）分解：将要解决的问题分解为若干个规模较小、相互独立、与原问题形式相同的子问题。

（2）治理：求解各个子问题。由于各个子问题与原问题形式相同，只是规模较小而已，而当子问题划分得足够小时，就可以用较简单的方法解决。

（3）合并：按原问题的要求，将子问题的解逐层合并构成原问题的解。

一言以蔽之，分治法就是将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

在分治算法中，各个子问题形式相同，解决的方法也一样，因此我们可以使用递归算法快速解决，递归是彰显分治法优势的利器。

3.2　猜数游戏——二分搜索技术

一天晚上，我们在家里看电视，某大型娱乐节目在玩猜数游戏。主持人在女嘉宾的手心上写一个10以内的整数，让女嘉宾的老公猜是多少，而女嘉宾只能提示大了，还是小了，并且只有3次机会。

主持人悄悄地在美女手心写了一个8。

老公：“2。”

老婆：“小了。”

老公：“3。”

老婆：“小了。”

老公：“10。”

老婆：“晕了!”

孩子说：“天啊，怎么还有这么笨的人。”那么，聪明的孩子，现在随机写1～n范围内的整数，你有没有办法以最快的速度猜出来呢？

图3-1　猜数游戏

3.2.1　问题分析

从问题描述来看，如果是n个数，那么最坏的情况要猜n次才能成功，其实我们没有必要一个一个地猜，因为这些数是有序的，它是一个二分搜索问题。我们可以使用折半查找的策略，每次和中间的元素比较，如果比中间元素小，则在前半部分查找（假定为升序），如果比中间元素大，则去后半部分查找。

3.2.2　算法设计

问题描述：给定n个元素，这些元素是有序的（假定为升序），从中查找特定元素x。

算法思想：将有序序列分成规模大致相等的两部分，然后取中间元素与特定查找元素x进行比较，如果x等于中间元素，则查找成功，算法终止；如果x小于中间元素，则在序列的前半部分继续查找，即在序列的前半部分重复分解和治理操作；否则，在序列的后半部分继续查找，即在序列的后半部分重复分解和治理操作。

算法设计：用一维数组S[]存储该有序序列，设变量low和high表示查找范围的下界和上界，middle表示查找范围的中间位置，x为特定的查找元素。

（1）初始化。令low=0，即指向有序数组S[]的第一个元素；high=n−1，即指向有序数组S[]的最后一个元素。

（2）middle=（low+high）/2，即指示查找范围的中间元素。

（3）判定low≤high是否成立，如果成立，转第4步，否则，算法结束。

（4）判断x与S[middle]的关系。如果x=S[middle]，则搜索成功，算法结束；如果x>S[middle]，则令low=middle+1；否则令high=middle−1，转为第2步。

3.2.3　完美图解

用分治法在有序序列（5，8，15，17，25，30，34，39，45，52，60）中查找元素17。

（1）数据结构。用一维数组S[]存储该有序序列，x=17，如图3-2所示。

图3-2　S[]数组

（2）初始化。low=0，high=10，计算middle=（low+high）/2=5，如图3-3所示。

图3-3　搜索初始化

（3）将x与S[middle]比较。x=17<S[middle]=30，我们在序列的前半部分查找，搜索的范围缩小到子问题S[0…middle−1]，令high=middle−1，如图3-4所示。

图3-4　搜索过程

（4）计算middle=（low+high）/2=2，如图3-5所示。

图3-5　搜索过程

（5）将x与S[middle]比较。x=17>S[middle]=15，我们在序列的后半部分查找，搜索的范围缩小到子问题S[middle+1…low]，令low=middle+1，如图3-6所示。

图3-6　搜索过程

（6）计算middle=（low+high）/2=3，如图3-7所示。

图3-7　搜索过程

（7）将x与S[middle]比较。x=17=S[middle]=17，查找成功，算法结束。

3.2.4　伪代码详解

我们用BinarySearch（int n，int s[]，int x）函数实现二分搜索技术，其中n为元素个数，s[]为有序数组，x为特定查找元素。low指向数组的第一个元素，high指向数组的最后一个元素。如果low≤high，middle=（low+high）/2，即指向查找范围的中间元素。如果x=S[middle]，搜索成功，算法结束；如果x>S[middle]，则令low=middle+1，去后半部分搜索；否则令high=middle−1，去前半部分搜索。

int BinarySearch(int n,int s[],int x)
{
    int low=0,high=n-1;          //low指向数组的第一个元素，high指向数组的最后一个元素
    while(low<=high)             //设置判定条件
    {
        int middle=(low+high)/2; //计算middle值(查找范围的中间值) 
        if(x==s[middle])         //x等于s[middle]，查找成功，算法结束
            return middle; 
        else if(x<s[middle])     //x小于s[middle]，则从前半部分查找
                high=middle-1; 
            else                 //x大于s[middle]，则从后半部分查找
                low=middle+1; 
    }
    return -1; 
}

3.2.5　实战演练

//program 3-1
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
using namespace std; 
const int M=10000; 
int x,n,i; 
int s[M]; 
int BinarySearch(int n,int s[],int x) 
{
    int low=0,high=n-1;         //low指向数组的第一个元素，high指向数组的最后一个元素
    while(low<=high) 
    {
         int middle=(low+high)/2; //middle为查找范围的中间值
         if(x==s[middle])      //x等于查找范围的中间值，算法结束
             return middle; 
         else if(x<s[middle])  //x小于查找范围的中间元素，则从前半部分查找
                  high=middle-1; 
                  else         //x大于查找范围的中间元素，则从后半部分查找
                  low=middle+1; 
    }
    return -1; 
}
int main()
{
     cout<<"请输入数列中的元素个数n为：";
     while(cin>>n) 
     {
           cout<<"请依次输入数列中的元素：";
           for(i=0;i<n;i++)
               cin>>s[i]; 
           sort(s,s+n); 
           cout<<"排序后的数组为：";
           for(i=0;i<n;i++)
           {
               cout<<s[i]<<" ";
           }
           cout<<endl; 
           cout<<"请输入要查找的元素：";
           cin>>x; 
           i=BinarySearch(n,s,x); 
           if(i==-1) 
              cout<<"该数列中没有要查找的元素"<<endl; 
           else
              cout<<"要查找的元素在第"<<i+1<<"位"<<endl; 
    }
    return 0; 
}

算法实现和测试

（1）运行环境

Code::Blocks

（2）输入

请输入数列中的元素个数n：11
请依次输入数列中的元素：60 1739 15 8 34 30 45 5 52 25

（3）输出

排序后的数组为：5 8 15 17 25 30 34 39 45 52 60
请输入要查找的元素：17
要查找的元素在第4位

3.2.6　算法解析与拓展

1．算法复杂度分析

（1）时间复杂度：首先需要进行排序，调用sort函数，进行排序复杂度为O(nlogn)，如果数列本身有序，那么这部分不用考虑。

然后是二分查找算法，时间复杂度怎么计算呢？如果我们用T(n)来表示n个有序元素的二分查找算法时间复杂度，那么：

• 当n=1时，需要一次比较，T(n)=O(1)。
• 当n>1时，特定元素和中间位置元素比较，需要O(1)时间，如果比较不成功，那么需要在前半部分或后半部分搜索，问题的规模缩小了一半，时间复杂度变为T(n/2)。

• 当n>1时，可以递推求解如下。

递推最终的规模为1，令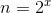，则。

二分查找算法的时间复杂度为O(logn)。

（2）空间复杂度：程序中变量占用了一些辅助空间，这些辅助空间都是常数阶的，因此空间复杂度为O(1)。

2．优化拓展

在上面程序中，我们采用BinarySearch（int n，int s[]，int x）函数来实现二分搜索，那么能不能用递归来实现呢？因为递归有自调用问题，那么就需要增加两个参数 low 和 high来标记搜索范围的开始和结束。

int recursionBS (int s[],int x,int low,int high) 
{
    //low指向数组的第一个元素，high指向数组的最后一个元素
    if(low>high)              //递归结束条件
        return -1; 
    int middle=(low+high)/2;  //计算middle值(查找范围的中间值) 
    if(x==s[middle])          //x等于s[middle]，查找成功，算法结束
        return middle; 
    else if(x<s[middle])      //x小于s[middle]，则从前半部分查找
             returnrecursionBS (s[],x, low, high-1) 
           else               //x大于s[middle]，则从后半部分查找
             returnrecursionBS (s[],x, middle+1, high) 
}

在主函数main()的调用中，只需要把BinarySearch（n，s，x）换为recursionBS（s[]，x，0，n−1）即可完成二分查找，递归算法的时间复杂度未变，因为递归调用需要使用栈来实现，空间复杂度怎么计算呢？

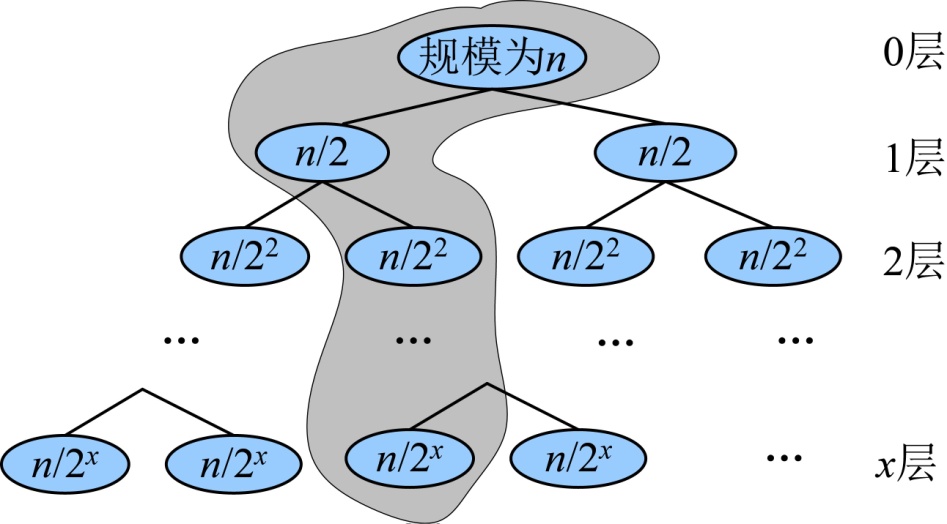
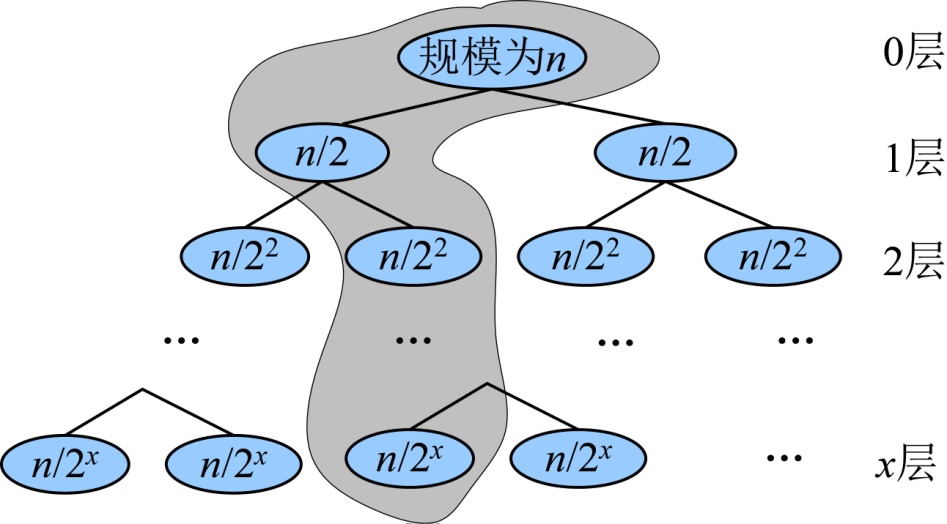
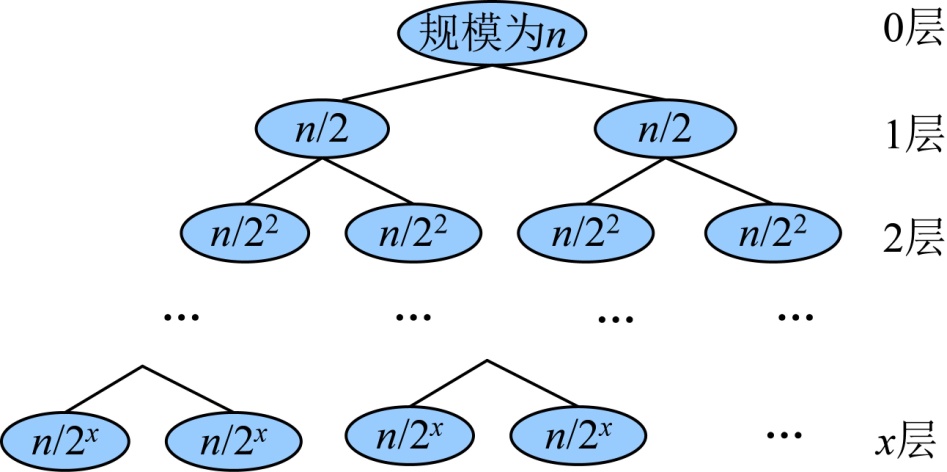
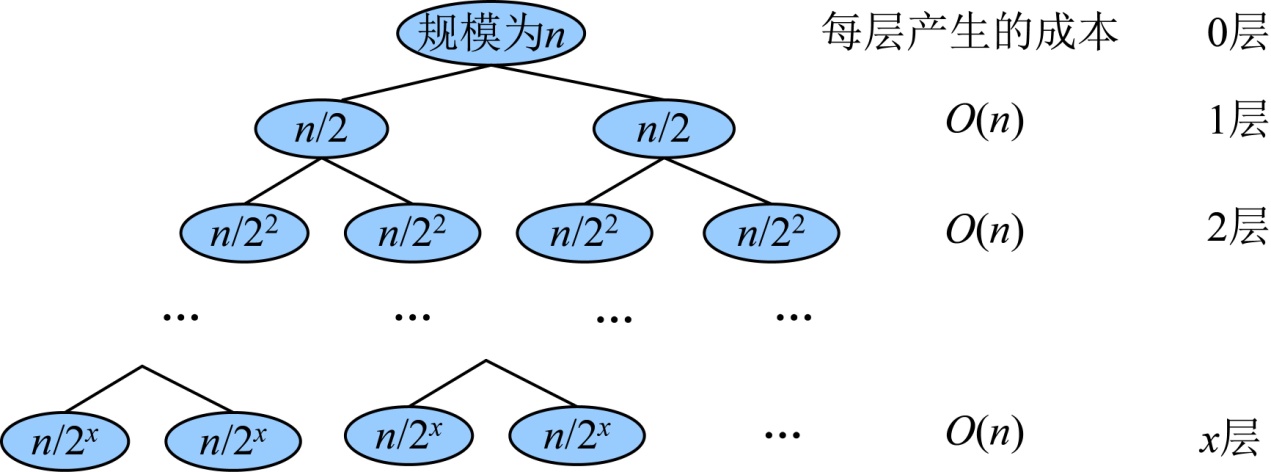
在递归算法中，每一次递归调用都需要一个栈空间存储，那么我们只需要看看有多少次调用。假设原问题的规模为n，那么第一次递归就分为两个规模为n/2的子问题，这两个子问题并不是每个都执行，只会执行其中之一。因为我们和中间值比较后，要么去前半部分查找，要么去后半部分查找；然后再把规模为n/2的子问题继续划分为两个规模为n/4的子问题，选择其一；继续分治下去，最坏的情况会分治到只剩下一个数值，那么我们执行的节点数就是从树根到叶子所经过的节点，每一层执行一个，直到最后一层，如图3-8所示。

图3-8　递归求解树

递归调用最终的规模为1，即n/2^x=1，则x=logn。假设阴影部分是搜索经过的路径，一共经过了logn个节点，也就是说递归调用了logn次。

因此，二分搜索递归算法的空间复杂度为O(logn)。

那么，还有没有更好的算法来解决这个问题呢？

3.3　合久必分，分久必合——合并排序

在数列排序中，如果只有一个数，那么它本身就是有序的；如果只有两个数，那么一次比较就可以完成排序。也就是说，数越少，排序越容易。那么，如果有一个由大量数据组成的数列，我们很难快速地完成排序，该怎么办呢？可以考虑将其分解为很小的数列，直到只剩一个数时，本身已有序，再把这些有序的数列合并在一起，执行一个和分解相反的过程，从而完成整个数列的排序。

图3-9　合并排序

3.3.1　问题分析

合并排序就是采用分治的策略，将一个大的问题分成很多个小问题，先解决小问题，再通过小问题解决大问题。由于排序问题给定的是一个无序的序列，可以把待排序元素分解成两个规模大致相等的子序列。如果不易解决，再将得到的子序列继续分解，直到子序列中包含的元素个数为1。因为单个元素的序列本身是有序的，此时便可以进行合并，从而得到一个完整的有序序列。

3.3.2　算法设计

合并排序是采用分治策略实现对n个元素进行排序的算法，是分治法的一个典型应用和完美体现。它是一种平衡、简单的二分分治策略，过程大致分为：

（1）分解——将待排序元素分成大小大致相同的两个子序列。

（2）治理——对两个子序列进行合并排序。

（3）合并——将排好序的有序子序列进行合并，得到最终的有序序列。

3.3.3　完美图解

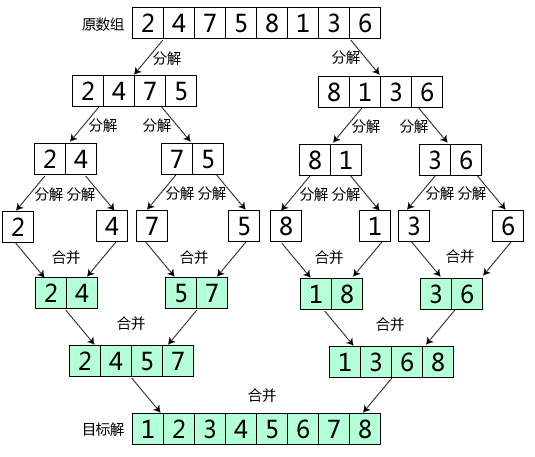
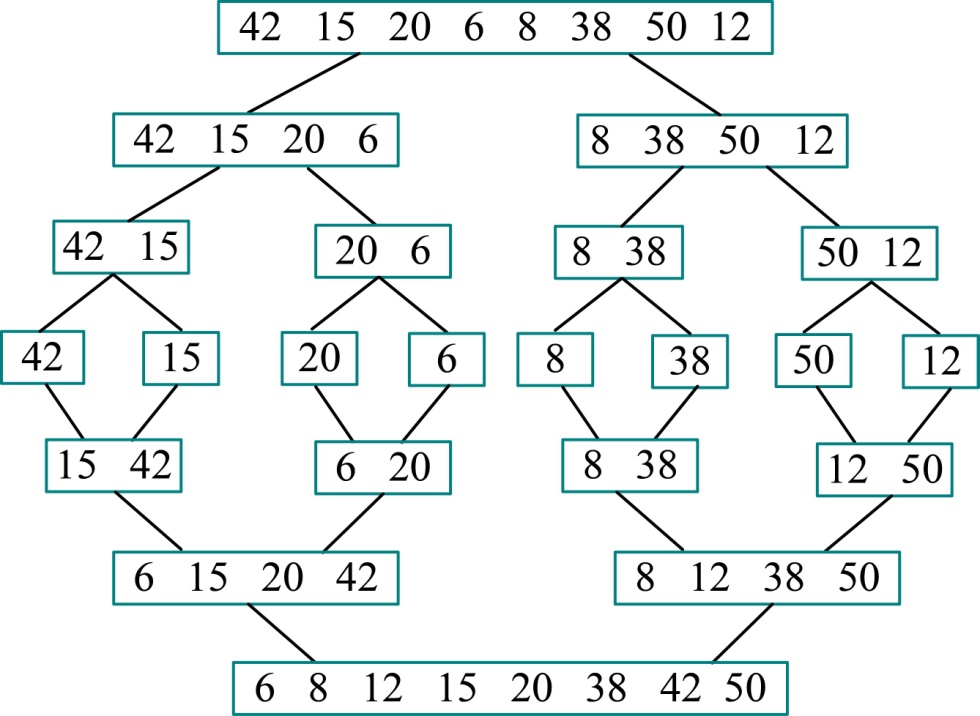
给定一个列数（42，15，20，6，8，38，50，12），我们执行合并排序的过程，如图3-10所示。

图3-10　合并排序过程

从上图可以看出，首先将待排序元素分成大小大致相同的两个子序列，然后再把子序列分成大小大致相同的两个子序列，如此下去，直到分解成一个元素停止，这时含有一个元素的子序列都是有序的。然后执行合并操作，将两个有序的子序列合并为一个有序序列，如此下去，直到所有的元素都合并为一个有序序列。

合久必分，分久必合！合并排序就是这个策略。

3.3.4　伪代码详解

（1）合并操作

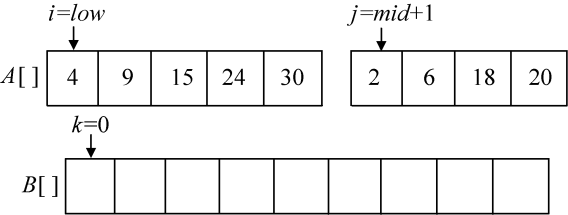
为了进行合并，引入一个辅助合并函数Merge（A，low，mid，high），该函数将排好序的两个子序列A[low:mid]和A[mid+1:high]进行合并。其中，low和high代表待合并的两个子序列在数组中的下界和上界，mid代表下界和上界的中间位置，如图3-11所示。

图3-11　合并操作原始数组

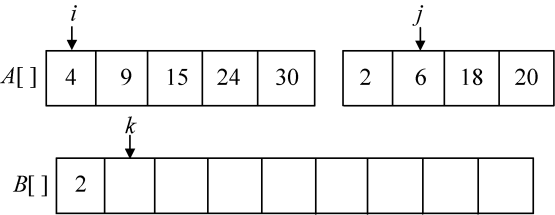
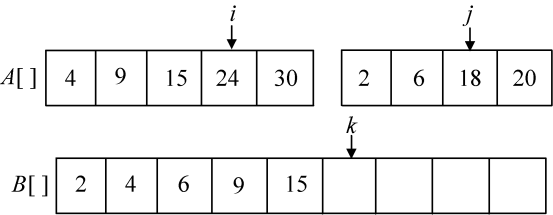
合并方法：设置3个工作指针i、j、k（整型数）和一个辅助数组B[]。其中，i和j分别指向两个待排序子序列中当前待比较的元素，k指向辅助数组B[]中待放置元素的位置。比较A[i]和A[j]，将较小的赋值给B[k]，同时相应指针向后移动。如此反复，直到所有元素处理完毕。最后把辅助数组B中排好序的元素复制到A数组中，如图3-12所示。

int *B = new int[high-low+1];//申请一个辅助数组B[]  
int i = low, j = mid+1, k = 0;

图3-12　合并操作初始化

现在，我们比较A[i]和A[j]，将较小的元素放入B数组中，相应的指针向后移动，直到i>mid或者j>high时结束。

while(i <= mid && j <= high)//按从小到大顺序存放到辅助数组B[]中
{
    if(A[i] <= A[j]) 
          B[k++] = A[i++];  
    else
          B[k++] = A[j++];  
}

第1次比较A[i]=4和A[j]=2，将较小元素2放入B数组中，j++，k++，如图3-13所示。

图3-13　合并过程

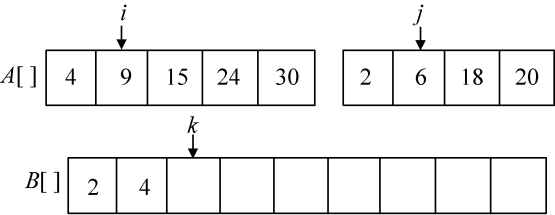
第2次比较A[i]=4和A[j]=6，将较小元素4放入B数组中，i++，k++，如图3-14所示。

图3-14　合并过程

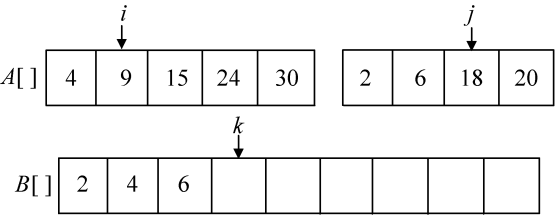
第3次比较A[i]=9和A[j]=6，将较小元素6放入B数组中，j++，k++，如图3-15所示。

图3-15　合并过程

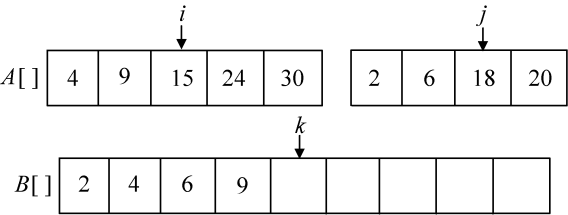
第4次比较A[i]=9和A[j]=18，将较小元素9放入B数组中，i++，k++，如图3-16所示。

图3-16　合并过程

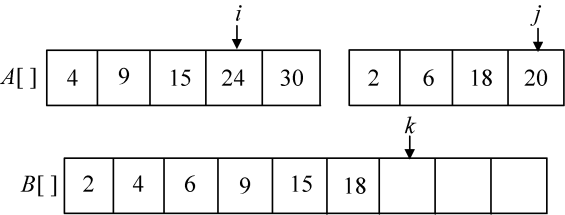
第5次比较A[i]=15和A[j]=18，将较小元素15放入B数组中，i++，k++，如图3-17所示。

图3-17　合并过程

第6次比较A[i]=24和A[j]=18，将较小元素18放入B数组中，j++，k++，如图3-18所示。

图3-18　合并过程

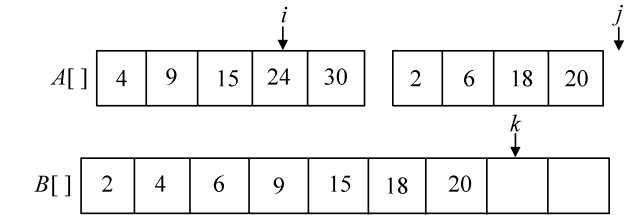
第7次比较A[i]=24和A[j]=20，将较小元素20放入B数组中，j++，k++，如图3-19所示。

图3-19　合并过程

此时，j>high了，while循环结束，但A数组还剩有元素（i≤mid）怎么办呢？直接放置到B数组就可以了，如图3-20所示。

while(i <= mid) B[k++] = A[i++];//对子序列A[low:middle]剩余的依次处理

图3-20　合并过程

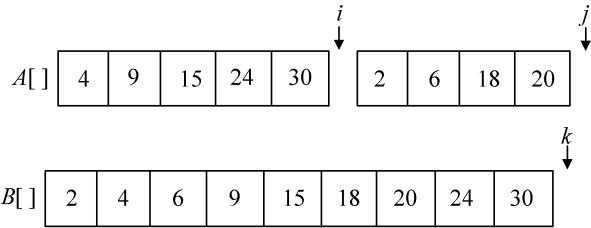
现在已经完成了合并排序的过程，还需要把辅助数组B中的元素复制到原来的A数组中，如图3-21所示。

for(i = low, k = 0; i <= high; i ++)//将合并后的有序序列复制到原来的A[]序列
   A[i] = B[k++];

图3-21　合并结果复制到A[]

完整的合并程序如下：

void Merge(int A[], int low, int mid, int high) 
{  
  int *B = new int[high-low+1];//申请一个辅助数组  
  int i = low, j = mid+1, k = 0;   
  while(i <= mid && j <= high) 
  {//按从小到大存放到辅助数组B[]中  
    if(A[i] <= A[j]) 
         B[k++] = A[i++];  
    else 
         B[k++] = A[j++];  
  }  
while(i <= mid) B[k++] = A[i++];       //对子序列A[low:middle]剩余的依次处理
while(j <= high) B[k++] = A[j++];      //对子序列A[middle+1:high]剩余的依次处理
for(i = low, k = 0; i <= high; i ++)   //将合并后的序列复制到原来的A[]序列
   A[i] = B[k++];
}

（2）递归形式的合并排序算法

将序列分为两个子序列，然后对子序列进行递归排序，再把两个已排好序的子序列合并成一个有序的序列。

void MergeSort(int A[], int low, int high) 
{  
  if(low < high) 
  {  
     int mid = (low+high)/2; 
     MergeSort(A, low, mid);           //对A[low:mid]中的元素合并排序  
     MergeSort(A, mid+1, high);        //对A[mid+1:high]中的元素合并排序  
     Merge(A, low, mid, high);         //合并操作
  }
}

3.3.5　实战演练

//program 3-2
#include <iostream>
#include <cstdlib>
#include <cstdio>
using namespace std; 
void Merge(int A[], int low, int mid, int high) 
{
     int *B = new int[high-low+1];     //申请一个辅助数组
     int i = low, j = mid+1, k = 0; 
     while(i <= mid && j <= high) 
{//按从小到大存放到辅助数组B[]中
         if(A[i] <= A[j]) 
               B[k++] = A[i++];
         else
               B[k++] = A[j++];
     }
     while(i <= mid) B[k++] = A[i++];  //将数组中剩下的元素复制到数组B中
     while(j <= high) B[k++] = A[j++];
     for(i = low, k = 0; i <= high; i ++)
           A[i] = B[k++];
}
void MergeSort(int A[], int low, int high) 
{
     if(low < high) 
{
           int mid = (low+high) /2;   //取中点
           MergeSort(A, low, mid);    //对A[low:mid]中的元素合并排序
           MergeSort(A, mid+1, high); //对A[mid+1:high]中的元素合并排序
           Merge(A, low, mid, high);  //合并
     }
}
int main()
{
     int n, A[100]; 
     cout<<"请输入数列中的元素个数n为："<<endl; 
     cin>>n; 
     cout<<"请依次输入数列中的元素："<<endl; 
     for(int i=0; i<n; i++)
          cin>>A[i]; 
     MergeSort(A,0,n-1); 
     cout<<"合并排序结果："<<endl; 
     for(int i=0;i<n;i++)
          cout<<A[i]<<" ";
     cout<<endl; 
     return 0; 
}

算法实现和测试

（1）运行环境

Code::Blocks

（2）输入

请输入数列中的元素个数n为：
8
请依次输入数列中的元素：
42 15 20 6 8 38 50 12

（3）输出

合并排序结果：
6 8 12 15 20 38 42 50

3.3.6　算法解析与拓展

1．算法复杂度分析

（1）时间复杂度

• 分解：这一步仅仅是计算出子序列的中间位置，需要常数时间O(1)。
• 解决子问题：递归求解两个规模为n/2的子问题，所需时间为2T(n/2)。
• 合并：Merge算法可以在O(n)的时间内完成。

所以总运行时间为：

当n>1时，可以递推求解：

递推最终的规模为1，令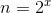，则，那么

合并排序算法的时间复杂度为O(nlogn)。

（2）空间复杂度：程序中变量占用了一些辅助空间，这些辅助空间都是常数阶的，每调用一个Merge()，会分配一个适当大小的缓冲区，且退出时释放。最多分配大小为n，所以空间复杂度为O(n)。递归调用所使用的栈空间是O(logn)，想一想为什么？

合并排序递归树如图3-22所示。

图3-22　合并排序递归树

递归调用时占用的栈空间是递归树的深度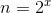，，则，递归树的深度为logn。

2．优化拓展

上面算法我们使用递归来实现，当然也可以使用非递归的方法，大家可以动手试试。

那么，还有没有更好的算法来解决这个问题呢？

3.4　兵贵神速——快速排序

未来的战争是科技的战争。假如A国受到B国的导弹威胁，那么A国就要启用导弹防御系统，根据卫星、雷达信息快速计算出敌方弹道导弹发射点和落点的信息，将导弹的跟踪和评估数据转告地基雷达，发射拦截导弹摧毁敌方导弹或使导弹失去攻击能力。如果A国的导弹防御系统处理速度缓慢，等算出结果时，导弹已经落地了，还谈何拦截？

现代科技的发展，速度至关重要。

我们以最基本的排序为例，生活中到处都用到排序，例如各种比赛、奖学金评选、推荐系统等，排序算法有很多种，能不能找到更快速高效的排序算法呢？

图3-23　某国导弹防御系统示意图

3.4.1　问题分析

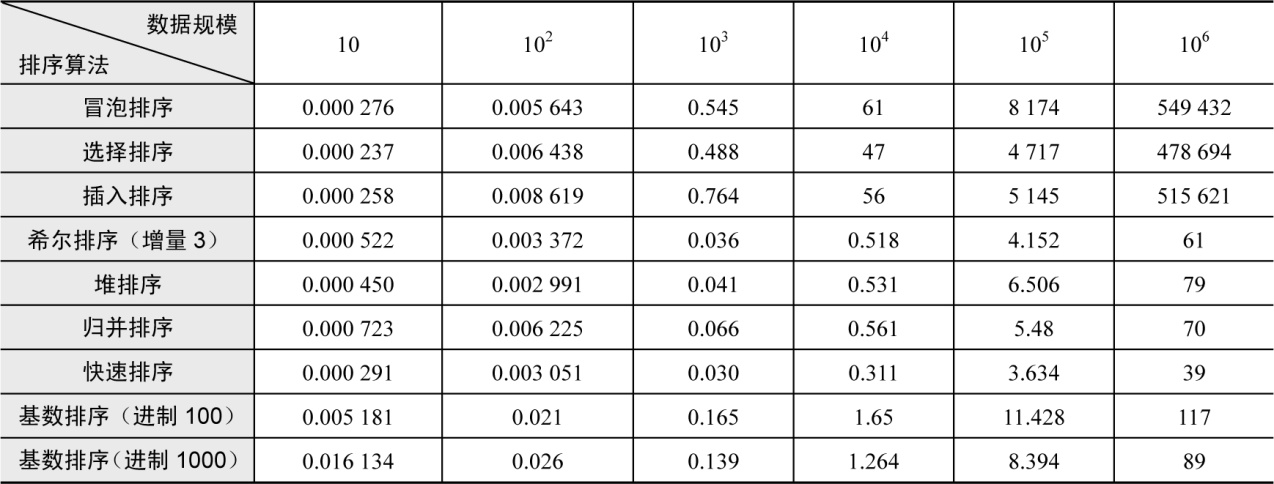
曾经有人做过实验，对各种排序算法效率做了对比（单位：毫秒），如表3-1所示。

表3-1　排序算法效率

从上面的表中我们可以看出，如果对10⁵个数据进行排序，冒泡排序需要8 174毫秒，而快速排序只需要3.634毫秒！

快速排序（Quicksort）是比较快速的排序方法。快速排序由C. A. R. Hoare在1962年提出。它的基本思想是通过一组排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此使所有数据变成有序序列。

我们前面刚讲过合并排序（又叫归并排序），它每次从中间位置把问题一分为二，一直划分到不能再分时，执行合并操作。合并排序的划分很简单，但合并操作就复杂了，需要额外的辅助空间（辅助数组），在辅助数组中完成合并排序后复制到原来的位置，它是一种异地排序的方法。合并排序分解容易，合并难，属于“先易后难”。而快速排序是原地排序，不需要辅助数组，但分解困难，合并容易，是“先苦后甜”型。

3.4.2　算法设计

快速排序的基本思想是基于分治策略的，其算法思想如下。

（1）分解：先从数列中取出一个元素作为基准元素。以基准元素为标准，将问题分解为两个子序列，使小于或等于基准元素的子序列在左侧，使大于基准元素的子序列在右侧。

（2）治理：对两个子序列进行快速排序。

（3）合并：将排好序的两个子序列合并在一起，得到原问题的解。

设当前待排序的序列为R[low:high]，其中low≤high，如果序列的规模足够小，则直接进行排序，否则分3步处理。

（1）分解：在R[low: high]中选定一个元素R[pivot]，以此为标准将要排序的序列划分为两个序列R[low:pivot−1]和R[pivot+1:high]，并使用序列R[low:pivot−1]中所有元素的值小于等于R[pivot]，序列R[pivot+1:high]中所有元素均大于R[pivot]，此时基准元素已经位于正确的位置，它无需参加后面的排序，如图3-24所示。

图3-24　快速排序分解

（2）治理：对于两个子序列R[low:pivot−1]和R[pivot+1:high]，分别通过递归调用快速排序算法来进行排序。

（3）合并：由于对R[low:pivot−1]和R[pivot+1:high]的排序是原地进行的，所以在R[low:pivot−1]和R[pivot+1:high]都已经排好序后，合并步骤无需做什么，序列R[low:high]就已经排好序了。

如何分解是一个难题，因为如果基准元素选取不当，有可能分解成规模为0和n−1的两个子序列，这样快速排序就退化为冒泡排序了。

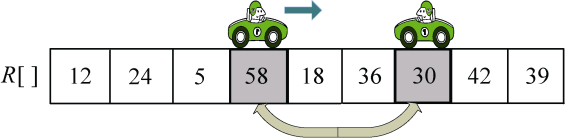
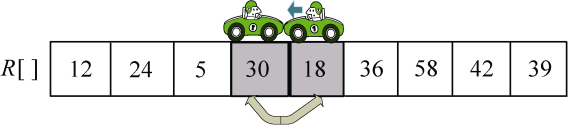
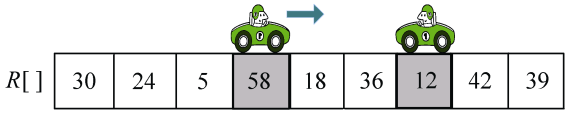
例如序列（30，24，5，58，18，36，12，42，39），第一次选取5做基准元素，分解后，如图3-25所示。

图3-25　选5做基准元素排序结果

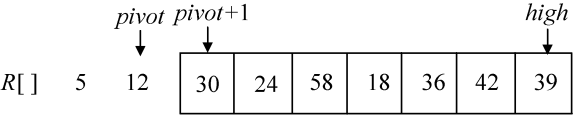
第二次选取12做基准元素，分解后如图3-26所示。

图3-26　继续选12做基准元素排序结果

是不是有点像冒泡了？这样做的效率是最差的，最理想的状态是把序列分解为两个规模相当的子序列，那么怎么选择基准元素呢？一般来说，基准元素选取有以下几种方法：

• 取第一个元素。
• 取最后一个元素。
• 取中间位置元素。
• 取第一个、最后一个、中间位置元素三者之中位数。
• 取第一个和最后一个之间位置的随机数k（low≤k≤high），选R[k]做基准元素。

3.4.3　完美图解

并没有明确的方法说哪一种基准元素选取方案最好，在此以选取第一个元素做基准为例，说明快速排序的执行过程。

假设当前待排序的序列为R[low:high]，其中low≤high。

步骤1：首先取数组的第一个元素作为基准元素pivot=R[low]。i=low，j=high。

步骤2：从右向左扫描，找小于等于pivot的数，如果找到，R[i]和R[j]交换，i++。

步骤3：从左向右扫描，找大于pivot的数，如果找到，R[i]和R[j]交换，j−−。

步骤4：重复步骤2～步骤3，直到i和j指针重合，返回该位置mid=i，该位置的数正好是pivot元素。

至此完成一趟排序。此时以mid为界，将原数据分为两个子序列，左侧子序列元素都比pivot小，右侧子序列元素都比pivot大，然后再分别对这两个子序列进行快速排序。

以序列（30，24，5，58，18，36，12，42，39）为例，演示排序过程。

（1）初始化。i=low，j=high，pivot=R[low]=30，如图3-27所示。

图3-27　快速排序初始化

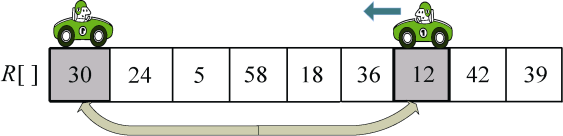
（2）向左走。从数组的右边位置向左找，一直找小于等于pivot的数，找到R[j]=12，如图3-28所示。

图3-28　快速排序过程（交换元素）

R[i]和R[j]交换，i++，如图3-29所示。

图3-29　快速排序过程（交换元素后）

（3）向右走。从数组的左边位置向右找，一直找比pivot大的数，找到R[i]=58，如图3-30所示。

图3-30　快速排序过程（交换元素）

R[i]和R[j]交换，j−−，如图3-31所示。

图3-31　快速排序过程（交换元素后）

（4）向左走。从数组的右边位置向左找，一直找小于等于pivot的数，找到R[j]=18，如图3-32所示。

图3-32　快速排序过程（交换元素）

R[i]和R[j]交换，i++，如图3-33所示。

图3-33　快速排序过程（交换元素后）

（5）向右走。从数组的左边位置向右找，一直找比pivot大的数，这时i=j，第一轮排序结束，返回i的位置，mid=i，如图3-34所示。

图3-34　第一趟快速排序（划分）结果

至此完成一轮排序。此时以mid为界，将原数据分为两个子序列，左侧子序列都比pivot小，右侧子序列都比pivot大。

然后再分别对这两个子序列（12，24，5，18）和（36，58，42，39）进行快速排序。

大家可以动手写一写哦！

3.4.4　伪代码详解

（1）划分函数

我们编写划分函数对原序列进行分解，分解为两个子序列，以基准元素pivot为界，左侧子序列都比pivot小，右侧子序列都比pivot大。先从右向左扫描，找小于等于pivot的数，找到后两者交换（r[i]和r[j]交换后i++）；再从左向右扫描，找比基准元素大的数，找到后两者交换（r[i]和r[j]交换后j−−）。扫描交替进行，直到i=j停止，返回划分的中间位置i。

int Partition(int r[],int low,int high)   //划分函数
{
     int i=low,j=high,pivot=r[low];       //基准元素
     while(i<j) 
     {
         while(i<j&&r[j]>pivot) 
             j--;                         //向左扫描
         if(i<j) 
         {
             swap(r[i++],r[j]);           //r[i]和r[j]交换后i右移一位
         }
         while(i<j&&r[i]<=pivot) 
             i++;                         //向右扫描
         if(i<j) 
         {
              swap(r[i],r[j--]);          //r[i]和r[j]交换后j左移一位
         }
     }
     return i;                            //返回最终划分完成后基准元素所在的位置
}

（2）快速排序递归算法

首先对原序列执行划分，得到划分的中间位置mid，然后以中间位置为界，分别对左半部分（low，mid−1）执行快速排序，右半部分（mid+1，high）执行快速排序。递归结束的条件是low≥high。

void QuickSort(int R[],int low,int high){ 
     int mid; 
     if(low<high) 
     {
          mid=Partition(R,low,high);      //返回基准元素位置
          QuickSort(R,low,mid-1);         //左区间递归快速排序
          QuickSort(R,mid+1,high);        //右区间递归快速排序
     }
}

3.4.5　实战演练

//program 3-3
#include <iostream>
using namespace std; 
int Partition(int r[],int low,int high) //划分函数
{
     int i=low,j=high,pivot=r[low];     //基准元素
     while(i<j) 
     {
          while(i<j&&r[j]>pivot) j--;   //向左扫描
          if(i<j) 
          {
               swap(r[i++],r[j]);       //r[i]和r[j]交换后i右移一位
          }
          while(i<j&&r[i]<=pivot) i++;  //向右扫描
          if(i<j) 
          {
               swap(r[i],r[j--]);       //r[i]和r[j]交换后j左移一位
          }
     }
     return i;                          //返回最终划分完成后基准元素所在的位置
}
void QuickSort(int R[],int low,int high)//快速排序递归算法
{
     int mid; 
     if(low<high) 
     {
          mid=Partition(R,low,high);    //基准位置
          QuickSort(R,low,mid-1);       //左区间递归快速排序
          QuickSort(R,mid+1,high);      //右区间递归快速排序
     }
}
int main()
{
     int a[1000]; 
     int i,N; 
     cout<<"请先输入要排序的数据的个数：";
     cin>>N; 
     cout<<"请输入要排序的数据：";
     for(i=0;i<N;i++)
          cin>>a[i]; 
     cout<<endl; 
     QuickSort(a,0,N-1); 
     cout<<"排序后的序列为："<<endl; 
     for(i=0;i<N;i++)
          cout<<a[i]<<" " ; 
     cout<<endl; 
     return 0; 
}

算法实现和测试

（1）运行环境

Code::Blocks

（2）输入

请先输入要排序的数据的个数：9
请输入要排序的数据：30 24 5 58 18 36 12 42 39

（3）输出

排序后的序列为：
5 12 18 24 30 36 39 42 58

3.4.6　算法解析与拓展

1．算法复杂度分析

（1）最好时间复杂度

• 分解：划分函数Partition需要扫描每个元素，每次扫描的元素个数不超过n，因此时间复杂度为O(n)。
• 解决子问题：在最理想的情况下，每次划分将问题分解为两个规模为n/2的子问题，递归求解两个规模为n/2的子问题，所需时间为2T(n/2)，如图3-35所示。

图3-35　快速排序最好的划分

• 合并：因为是原地排序，合并操作不需要时间复杂度，如图3-36所示。

图3-36　快速排序最好情况递归树

所以总运行时间为：

当n>1时，可以递推求解：

递推最终的规模为1，令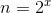，则，那么

快速排序算法最好的时间复杂度为O(nlogn)。

• 空间复杂度：程序中变量占用了一些辅助空间，这些辅助空间都是常数阶的，递归调用所使用的栈空间是O(logn)，想一想为什么？

（2）最坏时间复杂度

• 分解：划分函数Partition需要扫描每个元素，每次扫描的元素个数不超过n，因此时间复杂度为O(n)。
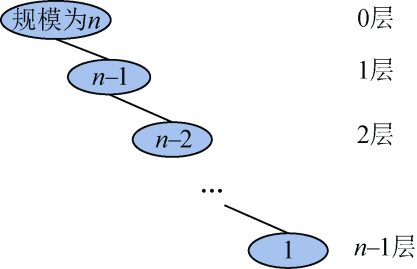
• 解决子问题：在最坏的情况下，每次划分将问题分解后，基准元素的左侧（或者右侧）没有元素，基准元素的另一侧为1个规模为n−1的子问题，递归求解这个规模为n−1的子问题，所需时间为T(n−1)。如图3-37所示。

图3-37　快速排序最坏的划分

• 合并：因为是原地排序，合并操作不需要时间复杂度。如图3-38所示。

图3-38　快速排序最坏情况递归树

所以总运行时间为：

当n>1时，可以递推求解如下：

快速排序算法最坏的时间复杂度为O(n²)。

• 空间复杂度：程序中变量占用了一些辅助空间，这些辅助空间都是常数阶的，递归调用所使用的栈空间是O(n)，想一想为什么？

（3）平均时间复杂度

假设我们划分后基准元素的位置在第 k（k=1，2，…，n）个，如图3-39所示。

图3-39　快速排序平均情况的划分

则：

由归纳法可以得出，T(n)的数量级也为O(nlogn)。快速排序算法平均情况下，时间复杂度为O(nlogn)，递归调用所使用的栈空间也是O(logn)。

2．优化拓展

从上述算法可以看出，每次交换都是在和基准元素进行交换，实际上没必要这样做，我们的目的就是想把原序列分成以基准元素为界的两个子序列，左侧子序列小于等于基准元素，右侧子序列大于基准元素。那么有很多方法可以实现，我们可以从右向左扫描，找小于等于pivot的数R[j]，然后从左向右扫描，找大于pivot的数R[i]，让R[i]和R[j]交换，一直交替进行，直到i和j碰头为止，这时将基准元素与R[i]交换即可。这样就完成了一次划分过程，但交换元素的个数少了很多。

假设当前待排序的序列为R[low: high]，其中low≤high。

步骤1：首先取数组的第一个元素作为基准元素pivot=R[low]。i=low，j=high。

步骤2：从右向左扫描，找小于等于pivot的数R[i]。

步骤3：从左向右扫描，找大于pivot的数R[j]。

步骤4：R[i]和R[j]交换，i++，j−−。

步骤5：重复步骤2～步骤4，直到i和j相等，如果R[i]大于pivot，则R[i−1]和基准元素R[low]交换，返回该位置mid=i−1；否则，R[i]和基准元素R[low]交换，返回该位置mid=i，该位置的数正好是基准元素。

至此完成一趟排序。此时以mid为界，将原数据分为两个子序列，左侧子序列元素都比pivot小，右侧子序列元素都比pivot大。

然后再分别对这两个子序列进行快速排序。

以序列（30，24，5，58，18，36，12，42，39）为例。

（1）初始化。i= low，j= high，pivot= R[low]=30，如图3-40所示。

图3-40　快速排序初始化

（2）向左走。从数组的右边位置向左找，一直找小于等于pivot的数，找到R[j]=12，如图3-41所示。

图3-41　快速排序过程（向左走）

（3）向右走。从数组的左边位置向右找，一直找比pivot大的数，找到R[i]=58，如图3-42所示。

图3-42　快速排序过程（向右走）

（4）R[i]和R[j]交换，i++，j−−，如图3-43所示。

图3-43　快速排序过程（交换元素）

（5）向左走。从数组的右边位置向左找，一直找小于等于pivot的数，找到R[j]=18，如图3-44所示。

图3-44　快速排序过程（向左走）

（6）向右走。从数组的左边位置向右找，一直找比pivot大的数，这时i=j，停止，如图3-45所示。

图3-45　快速排序过程（向右走）

（7）R[i]和R[low]交换，返回i的位置，mid=i，第一轮排序结束，如图3-46所示。

图3-46　快速排序过程（R[i]和R[low]交换）

至此完成一轮排序。此时以mid为界，将原数据分为两个子序列，左侧子序列都比pivot小，右侧子序列都比pivot大，如图3-47所示。

图3-47　快速排序第一次划分结果

然后再分别对这两个子序列（18，24，5，12）和（36，58，42，39）进行快速排序。

相比之下，上述的方法比每次和基准元素交换的方法更加快速高效！

优化后算法：

int Partition2(int r[],int low,int high)//划分函数
{
     int i=low,j=high,pivot=r[low];//基准元素
     while(i<j)
     {
           while(i<j&&r[j]>pivot) j--;//向左扫描
           while(i<j&&r[i]<=pivot) i++;//向右扫描
           if(i<j)
           {
                 swap(r[i++],r[j--]);//r[i]和r[j]交换，交换后i++, j--
           }
     }
     if(r[i]>pivot)
     {
           swap(r[i-1],r[low]);//r[i-1]和r[low]交换
           return i-1;//返回最终划分完成后基准元素所在的位置
    }
swap(r[i],r[low]);//r[i]和r[low]交换
    return i;//返回最终划分完成后基准元素所在的位置
}

大家可以思考是否还有更好的算法来解决这个问题呢？

3.5　效率至上——大整数乘法

在进行算法分析时，我们往往将加法和乘法运算当作一次基本运算处理，这个假定是建立在进行运算的整数能在计算机硬件对整数的表示范围内直接被处理的情况下，如果要处理很大的整数，则计算机硬件无法直接表示处理。那么我们能否将一个大的整数乘法分而治之？将大问题变成小问题，变成简单的小数乘法，这样既解决了计算机硬件处理的问题，又能够提高乘法的计算效率呢？

图3-48　大整数乘法

3.5.1　问题分析

有时，我们想要在计算机上处理一些大数据相乘时，由于计算机硬件的限制，不能直接进行相乘得到想要的结果。在解决两个大的整数相乘时，我们可以将一个大的整数乘法分而治之，将大问题变成小问题，变成简单的小数乘法再进行合并，从而解决上述问题。这样既解决了计算机硬件处理的问题，又能够提高乘法的计算效率。

例如：

继续分治：

我们可以看到当分解到只有一位数时，乘法就很简单了，如图3-49所示。

图3-49　大整数乘法分治图

3.5.2　算法设计

算法思想：解决本问题可以使用分治策略。

（1）分解

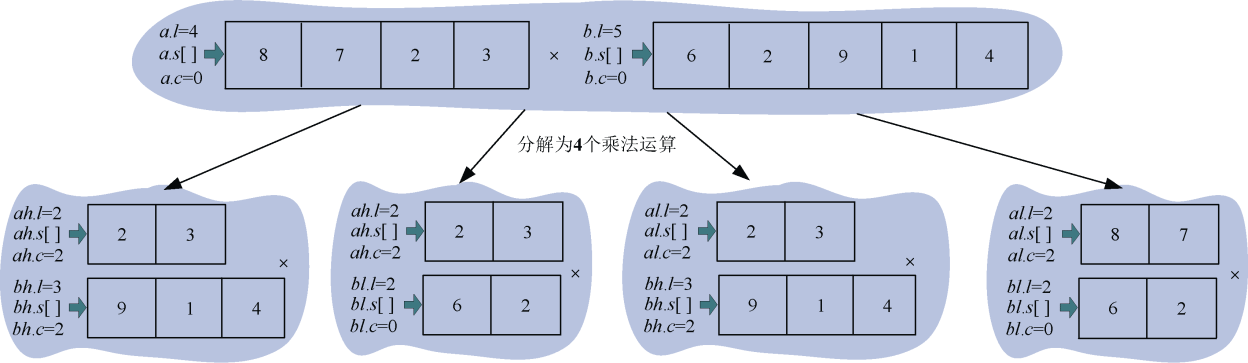
首先将2个大整数a（n位）、b（m位）分解为两部分，如图3-50所示。

图3-50　大整数a、b分解为高位和低位

ah表示大整数a的高位，al表示大整数a的低位。bh表示大整数b的高位，bl表示大整数b的低位。

ah、al为n/2位，bh、bl为m/2位。

2个大整数a（n位）、b（m位）相乘转换成了4个乘法运算ahbh、ahbl、albh、albl，而 乘数的位数变为了原来的一半 。

（2）求解子问题

继续分解每个乘法运算，直到分解有一个乘数为1位数时停止分解，进行乘法运算并记录结果。

（3）合并

将计算出的结果相加并回溯，求出最终结果。

3.5.3　完美图解

分治进行大整数乘法的道理非常简单，但具体怎么处理呢？

首先将两个大数以字符串的形式输入，转换成数字后， 倒序存储 在数组s[]中，l用来表示数的长度，c表示次幂。两个大数的初始次幂为0。

想一想，为什么要倒序存储，正序存储会怎样？

• cp()函数：用于将一个n位的数分成两个n/2的数并存储，记录它的长度和次幂。
• mul()函数：用于将两个数进行相乘，不断地进行分解，直到有一个乘数为1位数时停止分解，进行乘法运算并记录结果。
• add()函数：将分解得到的数进行相加合并。

例如：a=3278，b=41926，求a*b的值。

（1）初始化

将a、b 倒序存储 在数组a.s[]，b.s[]中，如图3-51所示。

图3-51　大整数a、b存储数组（倒序）

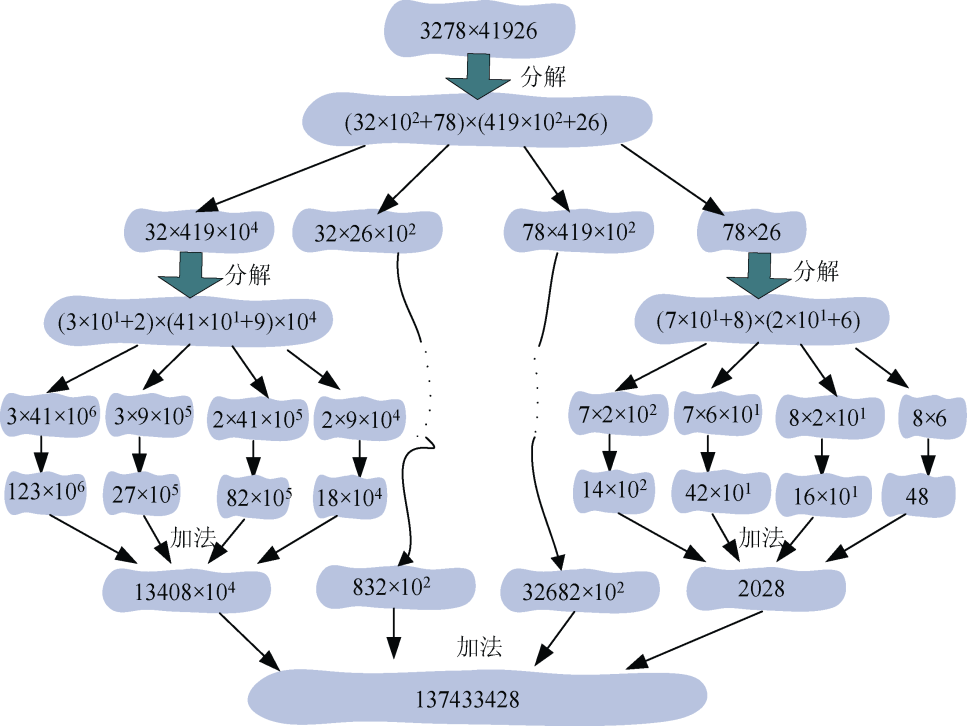
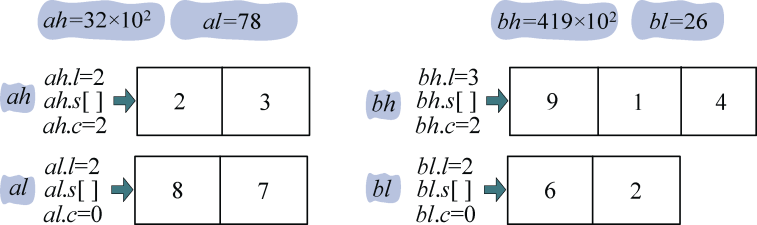
（2）分解

cp()函数用于将一个n位的数分成两个n/2的数并存储，记录它的长度和次幂。ah表示高位，al表示低位，l用来表示数的长度，c表示次幂，如图3-52所示。

图3-52　大整数a、b分解为高位和低位

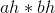
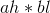
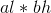
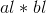
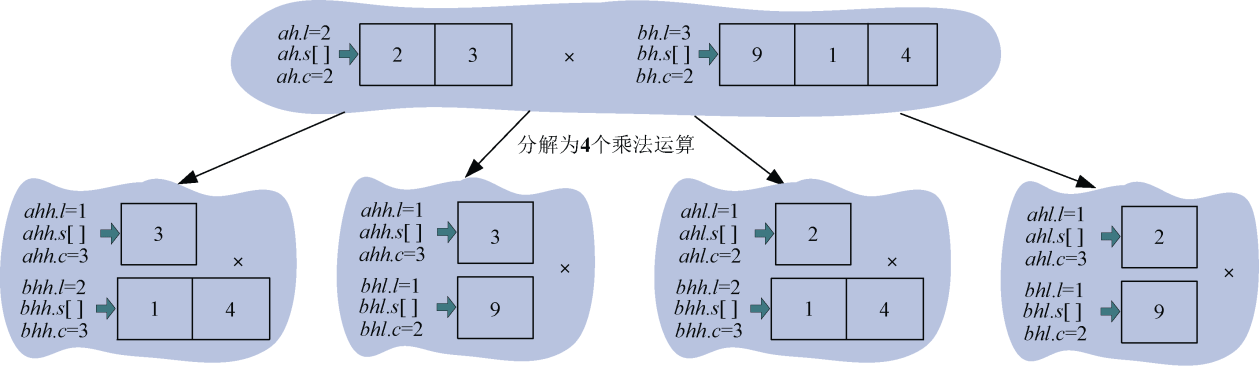
转换为4次乘法运算：，，，。如图3-53所示。

图3-53　原乘法分解为4次乘法

（3）求解子问题

，，，。下面以为例说明。如图3-54所示。

图3-54　ah*bh相乘分解

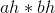
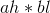
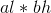
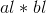
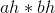
（4）继续求解子问题

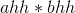
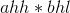
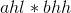
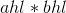
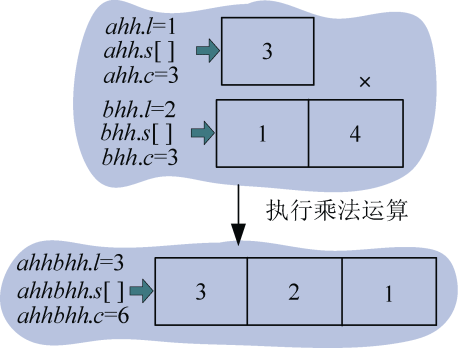
继续求解上面4个乘法运算，，，。可以看出这4个乘法运算都有一个乘数为1位数，可以直接进行乘法运算。

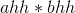
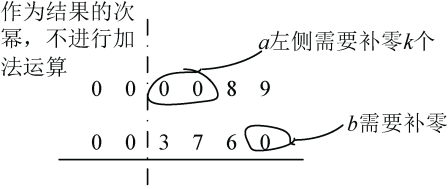
怎么进行乘法运算呢？以图3-53中为例，如图3-55所示。

图3-55　乘法运算

3首先和1相乘得到3存储在下面数组的第0位，然后3和4相乘得到12，那怎么存储呢，先存储12%10=2，然后存储进位12/10=1，这样乘法运算的结果是321， 注意是倒序 ，实际含义是3×41=123，还有一件事很重要，就是次幂！两数相乘时，结果的次幂是两个乘数次幂之和，3×10³×41×10³=123×10⁶。

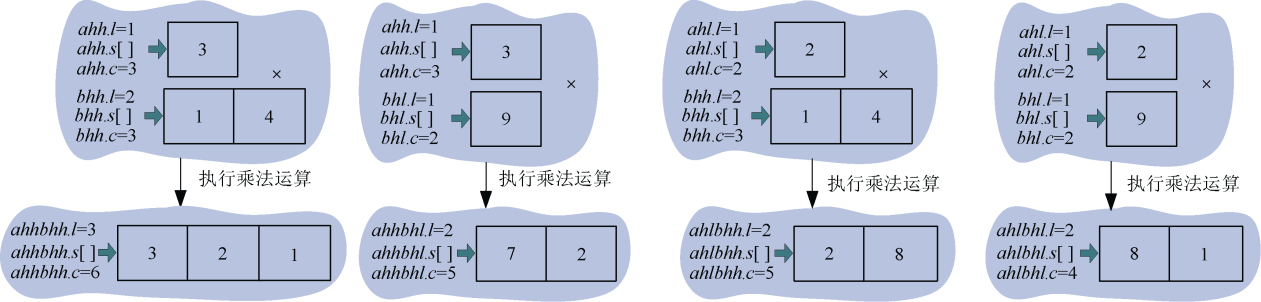
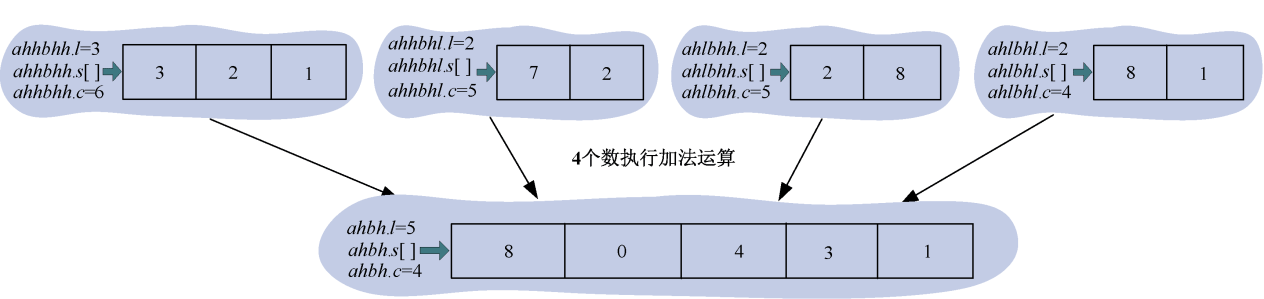
4个乘法运算结果如图3-56所示。

图3-56　4个乘法运算

（5）合并

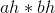
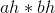
合并子问题结果，返回给 ，将上面4个乘法运算的结果加起来返回给。如图3-57所示。

图3-57　4个乘法运算结果相加

由此得到ah*bh=13408×10⁴。

用同样的方法求得ahbl=832×10²，albh=32682×10²，albl=2028。将这4个子问题结果加起来，合并得到原问题ab=137433428。

3.5.4　伪代码详解

（1）数据结构

将两个大数以字符串的形式输入，然后定义结构体Node，其中s[]数组用于存储大数， 注意是倒序存储！ （因为乘法加法运算中有可能产生进位，倒序存储时可以让进位存储在数组的末尾），l用于表示长度，c表示次幂。两个大数的初始次幂为0。

char sa[1000]; //接收大数的字符串
char sb[1000]; //接收大数的字符串
typedef struct _Node
{
     int s[M];  //数组，倒序存储大数
     int l;     //代表数的长度
     int c;     //代表数的次幂，例如32*105，那么将23存储在s[]中，l=2，c=5
} Node,*pNode; 

（2）划分函数

其中，cp()函数用于将一个n位的数分成两个n/2的数并存储，记录它的次幂。

void cp(pNode src, pNode des, int st, int l) 
{    //src表示待分解的数结点，des表示分解后得到的数结点
     //st表示从src结点数组中取数的开始位置，l表示取数的长度
     int i, j; 
     for(i=st, j=0; i<st+l; i++, j++) //从src结点数组中st位置开始，取l个数
     {
          des->s[j] = src->s[i];      //将这些数放入到des结点的数组中
     }
     des->l = l;                      //des长度等于取数的长度
     des->c = st + src->c;            //des次幂等于开始取数的位置加上src次幂
}

举例说明：如果有大数43579，我们首先把该数存储在结点a中，如图3-58所示。

ma = a.l/2;                           //ma表示a长度的一半，此例中a.l=5，ma=2

图3-58　大整数a存储数组（倒序）

分解得到a的高位ah，如图3-59所示。

cp(&a, &ah, ma, a.l-ma);              //相当于cp(a, &ah, 2, 3)；
          //即从a中数组第2个字符位置开始取3个字符，赋值给ah; 
          //ah的长度等于3；ah的次幂等于开始位置2加上a的次幂，即2+a.c=2

图3-59　大整数a的高位（倒序真实含义是435×10²）

然后分解得到a的低位al，如图3-60所示。

cp(&a, &al, 0, ma);                   //相当于cp(a, &al, 0, 2)；
          //即从a中数组第0个字符位置开始取2个字符，赋值给al; 
          //al的长度等于2；al的次幂等于开始位置0加上a的次幂，即0+a.c=0

图3-60　大整数a的低位（倒序真实含义是79）

这样两次调用cp()函数，我们就把一个大的整数分解成了两个长度约为原来一半的整数。

（3）乘法运算

定义的mul()函数用于将两个数进行相乘，不断地进行分解， 直到有一个乘数为1位时停止 ，让这两个数相乘，并记录结果回溯。

ma = pa->l/2; //ma表示a长度的一半
mb = pb->l/2; //mb表示b长度的一半
if(!ma || !mb) //如果!ma说明ma=0，即a的长度为1，该乘数为1位数
               //如果!mb说明mb=0，即b的长度为1，该乘数为1位数
{
     if(!ma)   //!ma说明a为1位数，a、b交换，保证a的长度大于等于b的长度
     {
          temp =pa; 
          pa = pb; 
          pb = temp; 
     }         //交换后b的长度为1
     ans->c = pa->c + pb->c;          //结果的次幂等于两乘数次幂之和
     w = pb->s[0];//因为交换后b的长度为1，用变量 w记录即可
     cc= 0;    //初始化进位cc为0
     for(i=0; i <pa->l; i++)          //把a中的数依次取出与w相乘，记录结果和进位
     {
         ans->s[i] = (w*pa->s[i] + cc)%10;//存储相乘结果的个位，十位做进位处理
         cc = (w*pa->s[i] + cc)/10;   //处理进位
     }

举例说明：两个数a=9×10²，b=87×10³相乘。a的数字为1位，a、b交换，保证a的长度大于等于b的长度，交换后a=87×10³，b=9×10²，倒序存储如图3-61所示。

图3-61　大整数a、b存储数组（倒序）

初始化进位cc=0。

先计算9×7=63，（63+cc）%10=3，ans−>s[0]=3，进位cc=（63+cc）/10=6。

再计算9×8=72，（72+cc）%10=8，ans−>s[1]=8，进位cc=（72+cc）/10=7。

a中的数处理完毕，退出for循环。

if(cc)                 //上例中退出时cc=7
    ans->s[i++] = cc;  //如果到最后还有进位，则存入数组末尾ans->s[2]=7
ans->l = i;            //记录结果的长度，上例中最后i=3

退出for循环时，cc不为0说明仍有进位，记录该进位，如图3-62所示。

图3-62　大整数a、b相乘结果（倒序）

ans结果为387，结果其实际含义是9×10²×87×10³=783×10⁵。

（4）合并函数

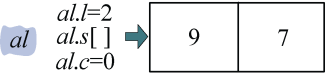
add()函数将分解得到的数进行相加合并。

void add(pNode pa, pNode pb, pNode ans) 
{   //程序调用时把 a、b地址传递给pa、pb参数，表示待合并的两个数
    //ans记录它们相加的结果
    int i, cc, k,alen,blen,len; 
    int ta, tb;         //ta、tb分别记录a、b相加时对应位上的数
    pNode temp; 
    if(pa->c <pb->c)    //交换以保证a的次幂大
    {
          temp = pa; 
          pa = b; 
          pb =temp; 
    }
    ans->c = pb->c;  //结果的次幂为两个数中小的次幂
    cc = 0;          //初始化进位cc为0
    k=pa->c - pb->c  //k为a左侧需要补零的个数

举例说明：两个数a=673×10²，b=98×10⁴相加。a的次幂为2，比b的次幂小，a、b交换，保证a的次幂大于等于b的次幂，交换后a=98×10⁴，b=673×10²，倒序存储如图3-63所示。

ans->c = pb->c;     //最低次幂作为结果的次幂，ans->c =pb->c=2
cc = 0;             //初始化进位cc为0
k= pa->c - pb->c;   //k为a左侧需要补零的个数，k=4-2=2

图3-63　大整数a、b存储数组（倒序）

如图3-64所示。

图3-64　大整数a、b加法

alen=pa->l + pa->c;       //a数加上次幂的总长度，上例中alen=6
blen=pb->l + pb->c;       //b数加上次幂的总长度，上例中alen= 5
if(alen>blen) 
      len=alen;           //取a、b总长度的最大值
else
      len=blen; 
len=len-pb->c;         //结果的长度为a，b之中的最大值减去最低次幂，上例中len= 4
             //最低次幂是不进行加法运算的位数) 
for(i=0; i<len; i++) 
{
     if(i <k)             //k为a左侧需要补零的个数
           ta = 0;        //a左侧补零
     else
           ta =pa->s[i-k];//i=k时，补0结束，从a数组中第0位开始取数字
     if(i <b->l) 
           tb = pb->s[i]; //从b数组中第0位开始取数字
     else
           tb = 0;        //b数字先取完，b右侧补0
     if(i>=pa->l+k)       //a数字先取完，a右侧补0
           ta = 0; 
     ans->s[i] = (ta + tb + cc)%10;  //记录两位之和的个位数，十位做进位处理
     cc = (ta + tb + cc)/10; 
}

如图3-65所示。

图3-65　大整数a、b加法结果

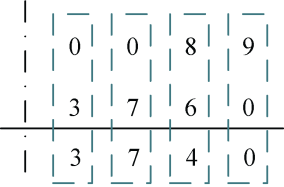
i=0时，ta=0，tb=3，ans->s[0] =（ta+tb+cc）%10=3，cc=（ta+tb+cc）/10=0。

i=1时，ta=0，tb=7，ans->s[1] =（ta+tb+cc）%10=7，cc=（ta+tb+cc）/10=0。

i=2时，ta=8，tb=6，ans->s[2] =（ta+tb+cc）%10=4，cc=（ta+tb+cc）/10=1。

i=3时，ta=9，tb=0，ans->s[3] =（ta+tb+cc）%10=0，cc=（ta+tb+cc）/10=1。

if(cc)    //如果上面退出时有进位，即cc不为0
     ans->s[i++] = cc;//有进位，则存入数组末尾ans->s[4]=1
ans->l = i;//上例中ans->l = 5;

如图3-66所示。

图3-66　大整数a、b加法结果存储数组

3.5.5　实战演练

//program 3-4
#include <stdlib.h>
#include <cstring>
#include <iostream>
using namespace std;
#define M 100
char sa[1000];
char sb[1000];
typedef struct _Node
{
     int s[M];
     int l;                 //代表字符串的长度
     int c;
} Node,*pNode;
void cp(pNode src, pNode des, int st, int l)
{
     int i, j;
     for(i=st, j=0; i<st+l; i++, j++)
     {
          des->s[j] = src->s[i];
     }
     des->l = l;
     des->c = st + src->c;  //次幂
}
void add(pNode pa, pNode pb, pNode ans)
{
     int i,cc,k,palen,pblen,len;
     int ta, tb;
     pNode temp;
     if((pa->c<pb->c))          //保证Pa的次幂大
     {
          temp = pa;
          pa = pb;
          pb = temp;
     }
     ans->c = pb->c;
     cc = 0;
     palen=pa->l + pa->c;
     pblen=pb->l + pb->c;
     if(palen>pblen)
          len=palen;
     else
          len=pblen;
     k=pa->c - pb->c;
     for(i=0; i<len-ans->c; i++) //结果的长度最长为pa，pb之中的最大长度减去最低次幂
     {
          if(i<k)
               ta = 0;
          else
               ta = pa->s[i-k];        //次幂高的补0，大于低的长度后与0进行计算
          if(i<pb->l)
               tb = pb->s[i];
          else
               tb = 0;
          if(i>=pa->l+k)
               ta = 0;
          ans->s[i] = (ta + tb + cc)%10;
          cc = (ta + tb + cc)/10;
     }
     if(cc)
          ans->s[i++] = cc;
     ans->l = i;
}
void mul(pNode pa, pNode pb, pNode ans)
{
     int i, cc, w;
     int ma = pa->l>>1, mb = pb->l>>1; //长度除2
     Node ah, al, bh, bl;
     Node t1, t2, t3, t4, z;
     pNode temp;
     if(!ma || !mb)                    //如果其中个数为1
     {
          if(!ma)  //如果a串的长度为1，pa,pb交换，pa的长度大于等于pb的长度
          {
               temp = pa;
               pa = pb;
               pb = temp;
          }
          ans->c = pa->c + pb->c;
          w = pb->s[0];
          cc = 0;                   //此时的进位为c
          for(i=0; i < pa->l; i++)
          {
               ans->s[i] = (w*pa->s[i] + cc)%10;
               cc= (w*pa->s[i] + cc)/10;
          }
          if(cc)
               ans->s[i++] = cc;   //如果到最后还有进位，则存入结果
          ans->l = i;              //记录结果的长度
          return;
     }
     //分治的核心
     cp(pa, &ah, ma, pa->l-ma);    //先分成4部分al,ah,bl,bh
     cp(pa, &al, 0, ma);
     cp(pb, &bh, mb, pb->l-mb);
     cp(pb, &bl, 0, mb);
     mul(&ah, &bh, &t1);           //分成4部分相乘
     mul(&ah, &bl, &t2);
     mul(&al, &bh, &t3);
     mul(&al, &bl, &t4);
     add(&t3, &t4, ans);
     add(&t2, ans, &z);
     add(&t1, &z, ans);
}
int main()
{
     Node ans,a,b;
     cout << "输入大整数 a："<<endl;
     cin >> sa;
     cout << "输入大整数 b："<<endl;
     cin >> sb;
     a.l=strlen(sa);               //sa,sb以字符串进行处理
     b.l=strlen(sb);
     int z=0,i;
     for(i = a.l-1; i >= 0; i--)
          a.s[z++]=sa[i]-'0';      //倒向存储
     a.c=0;
     z=0;
     for(i = b.l-1; i >= 0; i--)
          b.s[z++] = sb[i]-'0';
     b.c = 0;
     mul(&a, &b, &ans);
     cout << "最终结果为：";
     for(i = ans.l-1; i >= 0; i--)
          cout << ans.s[i];        //ans用来存储结果，倒向存储
     cout << endl;
     return 0;
}

算法实现和测试

（1）运行环境

Code::Blocks

Visual C++ 6.0

（2）输入

输入大整数a：
123456789
输入大整数b：
123456789

（3）输出

最终结果为：15241578750190521

3.5.6　算法解析与拓展

1．算法复杂度分析

（1）时间复杂度：我们假设大整数a、b都是n位数，根据分治策略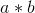，相乘将转换成了4个乘法运算ahbh、ahbl、albh、albl，而 乘数的位数变为了原来的一半 。直到最后递归分解到其中一个乘数为1位为止，每次递归就会使数据规模减小为原来的一半。假设两个n位大整数相乘的时间复杂度为T(n)，则：

当n>1时，可以递推求解如下：

递推最终的规模为1，令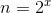则，那么有：

大整数乘法的时间复杂度为O(n²)。

（2）空间复杂度：程序中变量占用了一些辅助空间，都是常数阶的，但合并时结点数组占用的辅助空间为O(n)，递归调用所使用的栈空间是O(logn)，想一想为什么？

大整数乘法的空间复杂度为O(n)。

2．优化拓展

如果两个大整数都是n位数，那么有：

AB=ac10ⁿ+（ad+c*b）10^{n / 2}+bd

还记得快速算出1+2+3+…+100的小高斯吗？这孩子长大以后更聪明，他把4次乘法运算变成了3次乘法：

ad+cb=（a−b）（d−c）+ac+bd

AB= ac10 ⁿ +（（a−b）（d−c）+ac+b*d）10 ^{n / 2} +bd

这样公式中，就只有ac、（a−b）（d−c）、bd， 只需要进行3次乘法 。

那么时间复杂度为：

当n>1时，可以递推求解如下：

递推最终的规模为1，令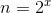，则，那么有：

优化改进后的大整数乘法的时间复杂度从O(n²)降为O(n^1.59)，这是一个巨大的改进！

但是 需要注意 ：在上面的公式中，A和B必须2ⁿ位。很容易证明，如果不为2ⁿ，那么A或者B在分解过程中必会出现奇数，那么ac和（（a−b）（d−c）+ac+b*d）的次幂就有可能不同，无法变为3次乘法了，解决方法也很简单，只需要补齐位数即可，在数前（高位）补0。

3.6　分治算法复杂度求解秘籍

分治法的道理非常简单，就是把一个大的复杂问题分为a（a>1）个形式相同的子问题，这些子问题的规模为n/b，如果分解或者合并的复杂度为f(n)，那么总的时间复杂度可以表示为：

那么如何求解时间复杂度呢？

上面的求解方式都是递推求解，写出其递推式，最后求出结果。

例如，合并排序算法的时间复杂度递推求解如下：

递推最终的规模为1，令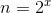，则，那么有：

1．递归树求解法

递归树求解方式其实和递推求解一样，只是递归树更清楚直观地显示出来，更能够形象地表达每层分解的结点和每层产生的成本。例如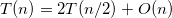：，如图3-67所示。

时间复杂度=叶子数*T(1)+成本和=。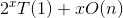

图3-67　分治递归树

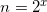
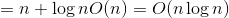
因为，则，那么时间复杂度=。

2．大师解法

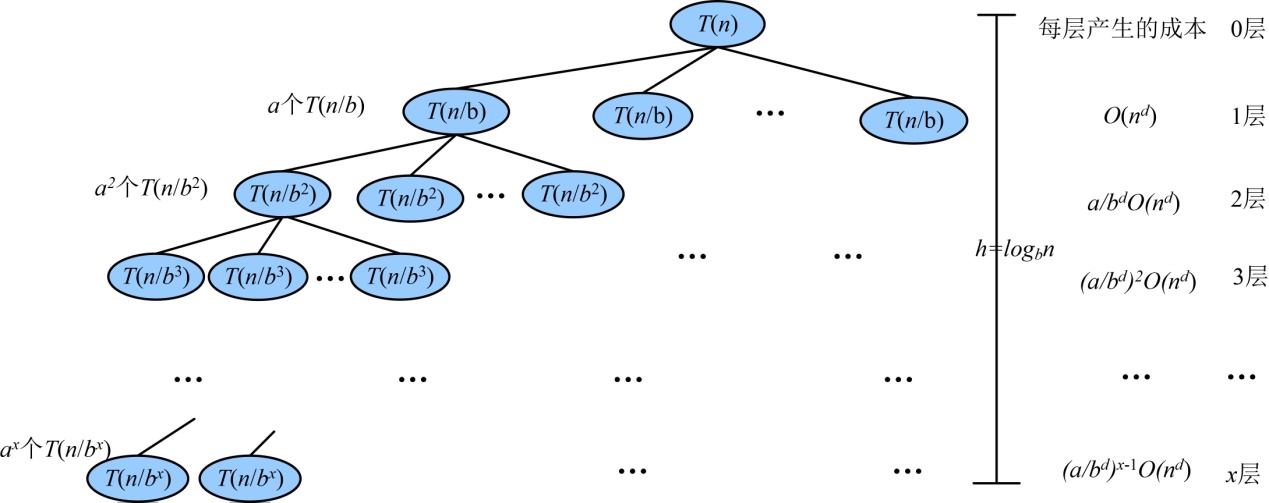
我们用递归树来说明大师解法：

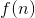
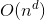
如果的数量级是，那么原公式转化为，如图3-68所示。

图3-68　大师解法递归树

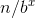
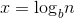
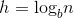
递归最终的规模为1，令=1，那么，即树高。

叶子数：。

成本和：。

时间复杂度=叶子数*T(1)+成本和

第1层成本：。

最后1层成本：

最后1层成本约等于叶子数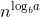，既然最后一层成本约等于叶子数，那么叶子数*T(1)就可以省略了，即 时间复杂度=成本和。

现在我们只需要观察每层产生的成本的发展趋势，是递减的还是递增的，还是每层都一样？每层成本的公比为。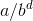

（1）每层成本是递减的（a/b^d<1）那么时间复杂度在渐进趋势上，成本和可以按 第1层 计算，其他忽略不计，即 时间复杂度 为：

（2）每层成本是递增的（a/b^d>1)那么时间复杂度在渐进趋势上，成本和可以按 最后1层 计算，其他忽略不计，即 时间复杂度 为：

（3）每层成本是相同的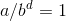（)，那么时间复杂度在渐进趋势上，每层成本都一样，我们把 第一层的成本乘以树高 即可。 时间复杂度 为：

形如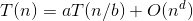的时间复杂度 求解秘籍 ：

举例如下。

• 猜数游戏

a=1，b=2，d=0，公比a/b^d=1，则。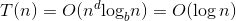

• 快速排序

a=2，b=2，d=1，公比a/b^d=1，则。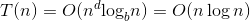

• 大整数乘法

a=4，b=2，d=1，公比a/b^d>1，则。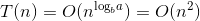

• 大整数乘法改进算法

a=3，b=2，d=1，公比a/b^d>1，则。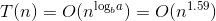

那么，如果时间复杂度公式不是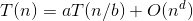怎么办呢？

画出递归树，观察每层产生的成本：

成本的公比小于1，时间复杂度按 第1层 计算；

成本的公比大于1，时间复杂度按 最后1层 计算；

成本的公比等于1，时间复杂度按 第1层*树高 计算。

以求解为例。

递推式解法如下：

大师解法如下：

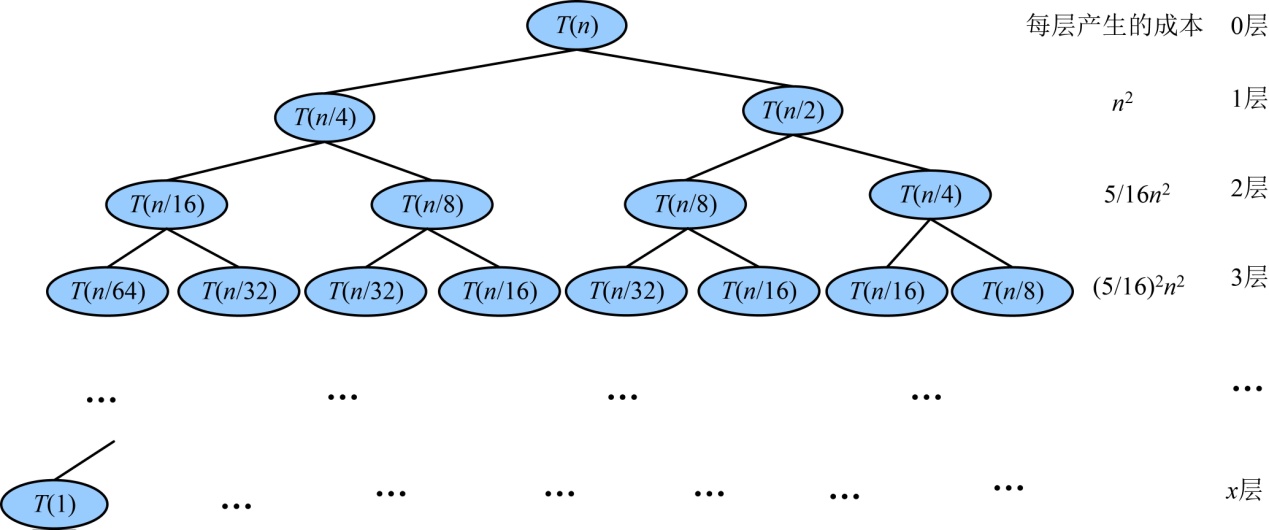
递归树如图3-69所示。

图3-69　大师解法递归树

首先从递归树中观察每层产生的成本发展趋势，每层的成本有时不是那么有规律，需要仔细验证。例如第3层是(5/16)²n²，需要验证第4层是(5/16)³n²。经过验证，我们发现每层成本是一个等比数列，公比为5/16（小于1），呈递减趋势，那么只计算第1项即可，时间复杂度为T(n)=O(n²)。