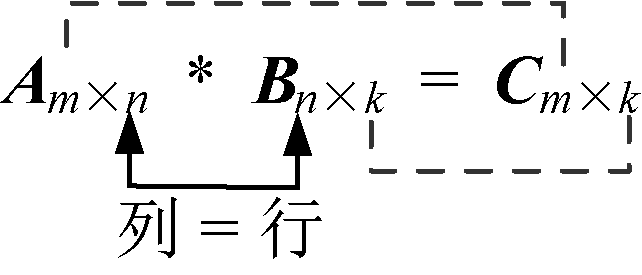
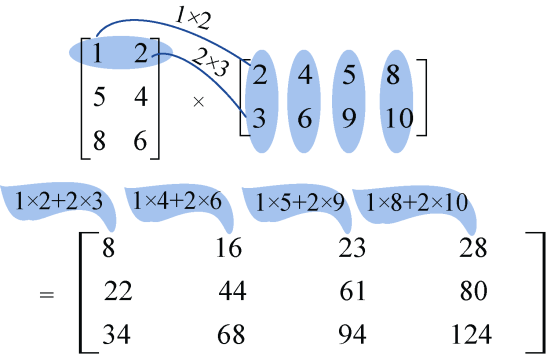
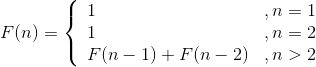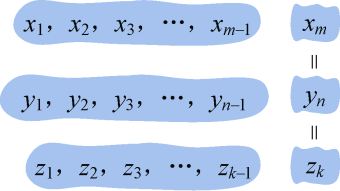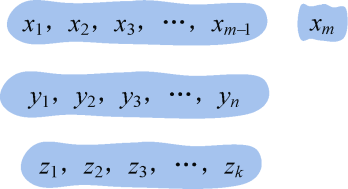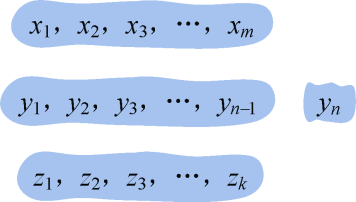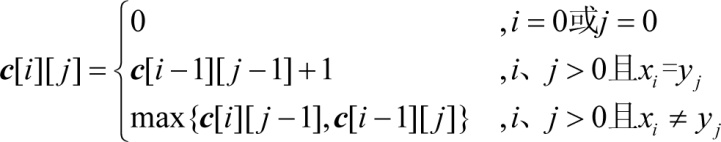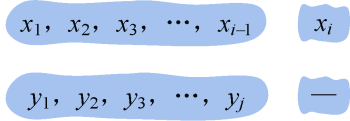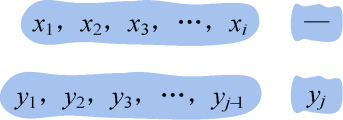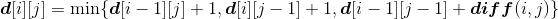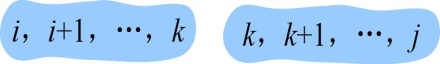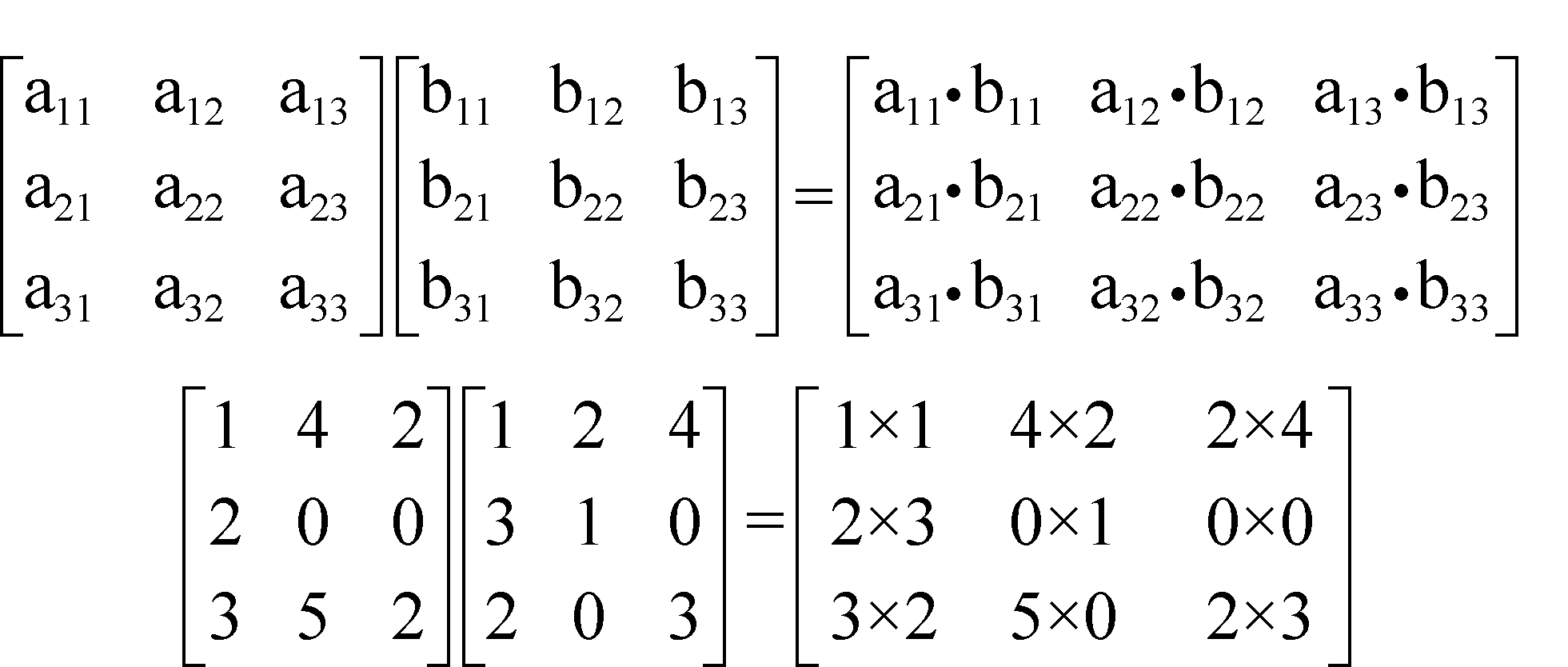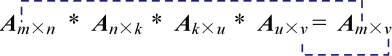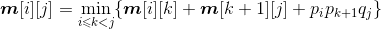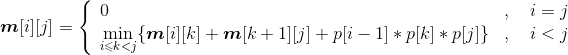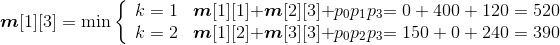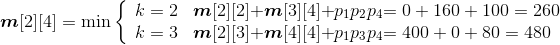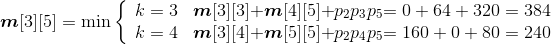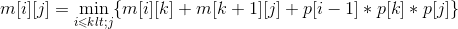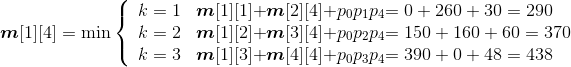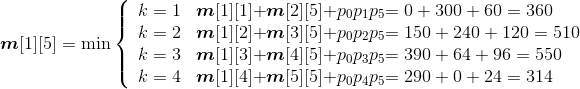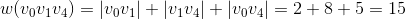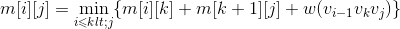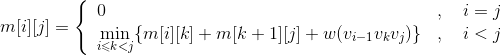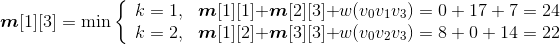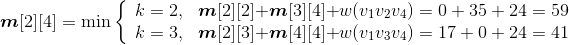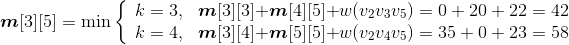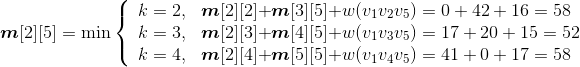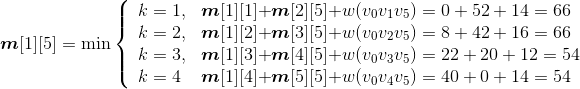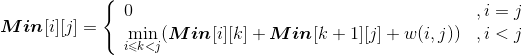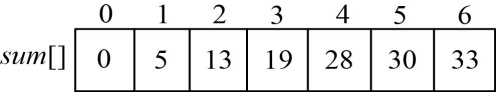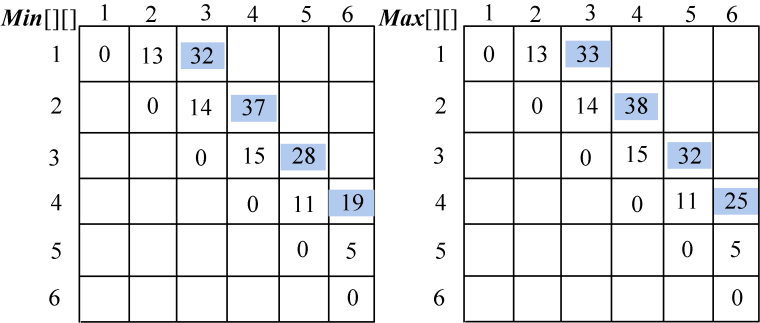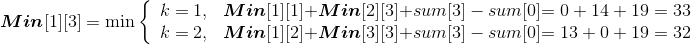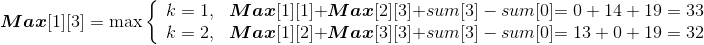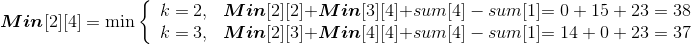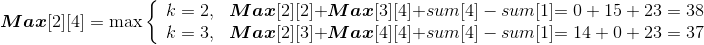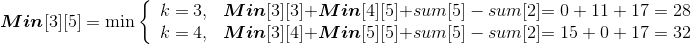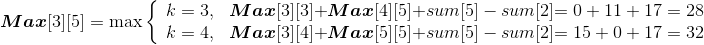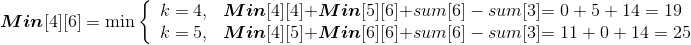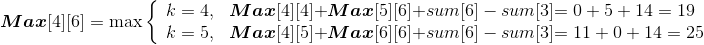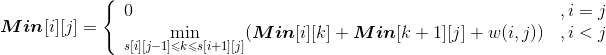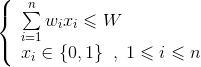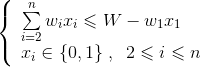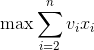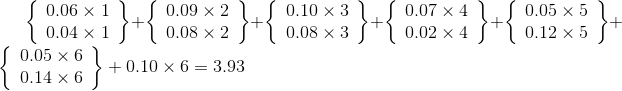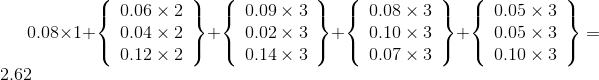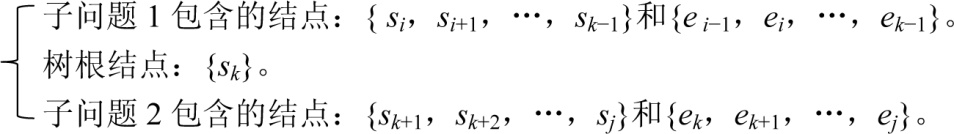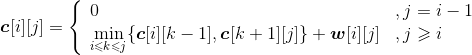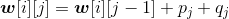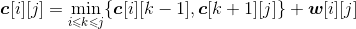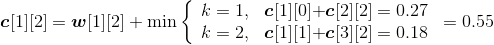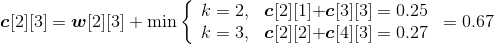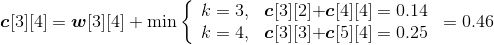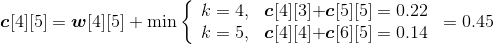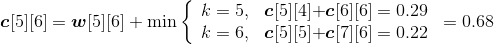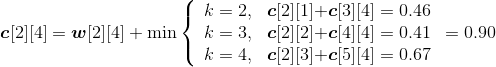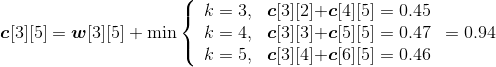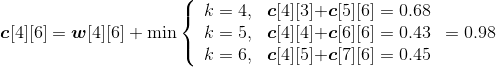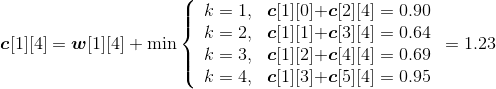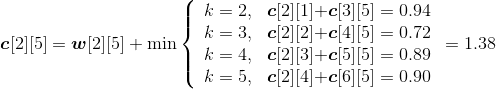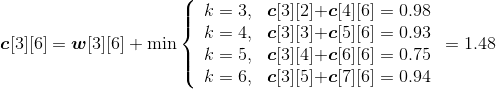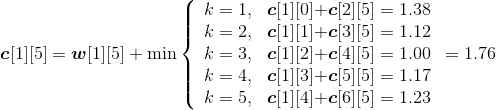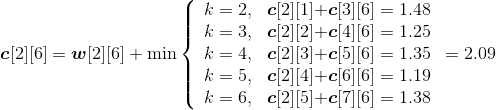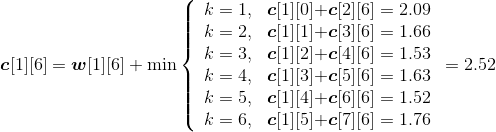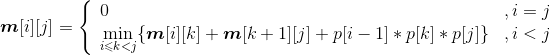《趣学算法》——第四章(动态规则)
第四章 动态规划
前面讲的分治法是将原问题分解为若干个规模较小、形式相同的子问题,然后求解这些子问题,合并子问题的解得到原问题的解。在分治法中,各个子问题是互不相交的,即相互独立。如果各个子问题有重叠,不是相互独立的,那么用分治法就重复求解了很多子问题,根本显现不了分治的优势,反而降低了算法效率。那该怎么办呢?
动态规划闪亮登场了!
4.1 神奇的兔子序列
公元1202年,意大利数学家列昂纳多•斐波那契(Leonardo Fibonacci)在《算盘全书》(Liber Abaci)中描述了一个神奇的兔子序列,这就是著名的斐波那契序列。
假设第1个月有1对刚诞生的兔子,第2个月进入成熟期,第3个月开始生育兔子,而1对成熟的兔子每月会生1对兔子,兔子永不死去……那么,由1对初生兔子开始,12个月后会有多少对兔子呢?如果是N对初生的兔子开始,M月后又会有多少对兔子呢?
第1个月,兔子①没有繁殖能力,所以还是 1 对。
第2个月,兔子①进入成熟期,仍然是 1 对。
第3个月,兔子①生了1对小兔②,于是这个月共有2对( 1+1=2 )兔子。
第4个月,兔子①又生了1对小兔③。兔子②进入成熟期。共有3对( 1+2=3 )兔子。
第5个月,兔子①又生了1对小兔④,兔子②也生下了1对小兔⑤。兔子③进入成熟期。共有5对( 2+3=5 )兔子。
第6个月,兔子①②③各生下了1对小兔。兔子④⑤进入成熟期。新生3对兔子加上原有的5对兔子,这个月共有8对( 3+5=8 )兔子。
……
这个数列有十分明显的特点,从第3个月开始,当月的兔子数=上月兔子数+本月新生小兔子数,而本月新生的兔子正好是上上月的兔子数,即当月的兔子数=前两月兔子之和。
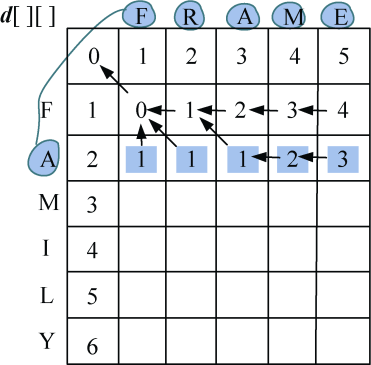
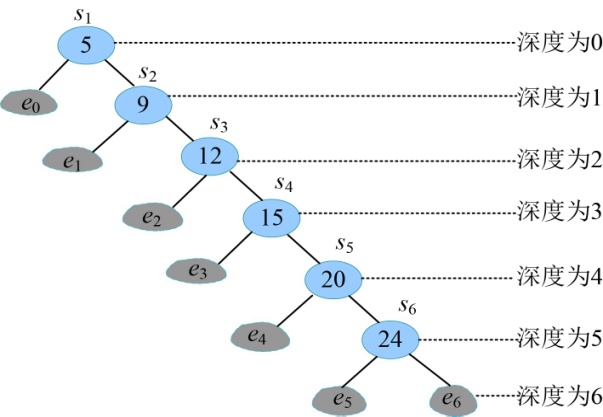
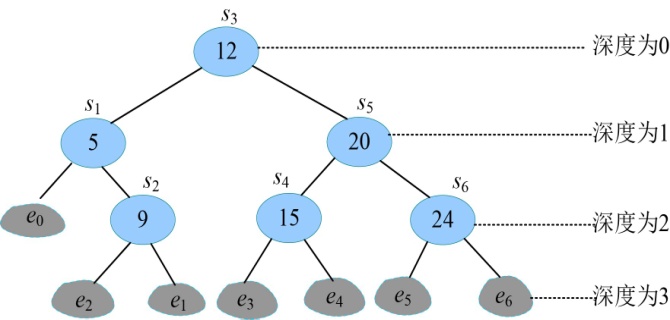
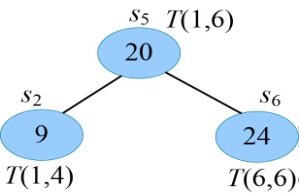
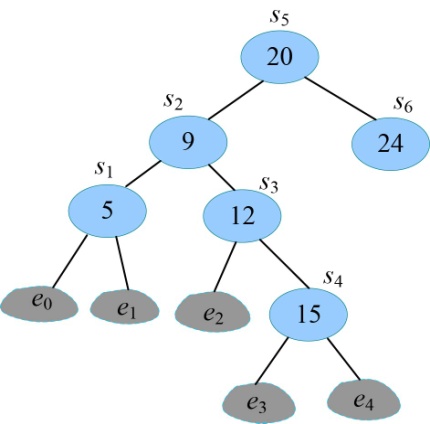
我们仅以F(6)为例,如图4-1所示。
从图4-1可以看出,有大量的结点重复(子问题重叠),F(4)、F(3)、F(2)、F(1)均重复计算多次。
4.2 动态规划基础
动态规划是1957年理查德•贝尔曼在《Dynamic Programming》一书中提出来的,可能有的读者不知道这个人,但他的一个算法你可能听说过,他和莱斯特•福特一起提出了求解最短路径的Bellman-Ford 算法,该算法解决了Dijkstra算法不能处理的负权值边的问题。
《Dynamic Programming》中的“Programming”不是编程的意思,而是指一种表格处理法。我们把每一步得到的子问题结果存储在表格里,每次遇到该子问题时不需要再求解一遍,只需要查询表格即可。
4.2.1 算法思想
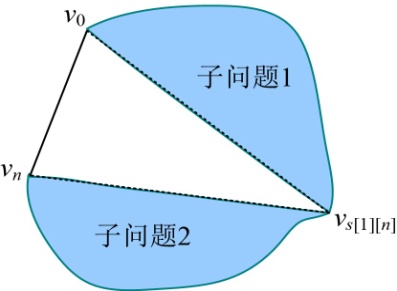
动态规划也是一种分治思想,但与分治算法不同的是,分治算法是把原问题分解为若干子问题,自顶向下求解各子问题,合并子问题的解,从而得到原问题的解。动态规划也是把原问题分解为若干子问题,然后自底向上,先求解最小的子问题,把结果存储在表格中,再求解大的子问题时,直接从表格中查询小的子问题的解,避免重复计算,从而提高算法效率。
4.2.2 算法要素
什么问题可以使用动态规划呢?我们首先要分析问题是否具有以下两个性质:
(1)最优子结构
最优子结构性质是指问题的最优解包含其子问题的最优解。最优子结构是使用动态规划的最基本条件,如果不具有最优子结构性质,就不可以使用动态规划解决。
(2)子问题重叠
子问题重叠是指在求解子问题的过程中,有大量的子问题是重复的,那么只需要求解一次,然后把结果存储在表中,以后使用时可以直接查询,不需要再次求解。子问题重叠不是使用动态规划的必要条件,但问题存在子问题重叠更能够充分彰显动态规划的优势。
4.2.3 解题秘籍
遇到一个实际问题,如何采用动态规划来解决呢?
(1)分析最优解的结构特征。
(2)建立最优值的递归式。
(3)自底向上计算最优值,并记录。
(4)构造最优解。
以神奇的兔子序列问题为例。
(1)分析最优解的结构特征
我们通过分析发现,前两个月都是1对兔子,而从第3个月开始,当月的兔子数等于前两个月的兔子数,如果把每个月的兔子数看作一个最小的子问题,那么求解第n个月的兔子数,包含了第n−1个月的兔子数和第n−2个月的兔子数这两个子问题。
(2)根据最优解结构特征,建立递归式
(3)自底向上计算最优值
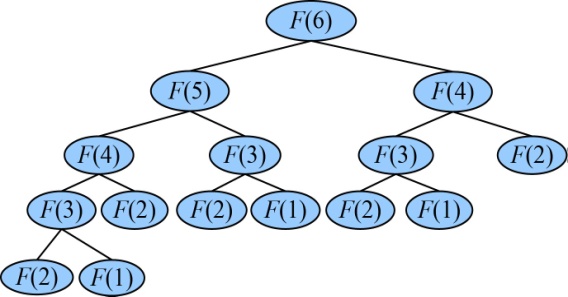
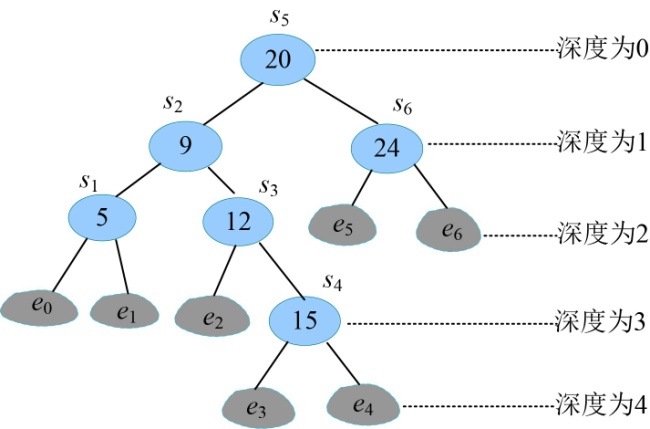
看到递归式,我们也很难立即求解F(n),如果直接递归调用将会产生大量的子问题重复,那怎么办呢?动态规划提供了一个好办法,自底向上求解,记录结果,重复的问题只需求解一次即可,如图4-2所示。
例如:
F(1)=1
F(2)=1
F(3)= F(2)+F(1)=2
F(4)= F(3)+F(2)=3
F(5)= F(4)+F(3)=5
F(6)= F(5)+F(4)=8
1 | int Fib2(int n) |
(4)构造最优解
本题中自底向上求解到树根就是我们要的最优解。
在众多的算法中,很多读者觉得动态规划是比较难的算法,为什么呢?难在递归式!
很多复杂问题,很难找到相应的递归式。实际上,一旦得到递归式,那算法就已经实现了99%,剩下的程序实现就非常简单了。那么后面的例子就重点讲解遇到一个问题怎么找到它的递归式。
蛇打三寸,一招致命。
4.3 孩子有多像爸爸——最长的公共子序列
假设爸爸对应的基因序列为X={x1,x2,x3,…,xm},孩子对应的基因序列Y={y1,y2,y3,…,yn},那么怎么找到他们有多少相似的基因呢?
如果按照严格递增的顺序,从爸爸的基因序列X中取出一些值,组成序列Z={xi1,xi2,xi3,…,xik},其中下标{i1,i2,i3,…,ik }是一个严格递增的序列。那么就说Z是X的子序列,Z中元素的个数就是该子序列的长度。
X和Y的公共子序列是指该序列既是X的子序列,也是Y的子序列。
最长公共子序列问题是指:给定两个序列X={x1,x2,x3,…,xm}和Y={y1,y2,y3,…,yn},找出X和Y的一个最长的公共子序列。
4.3.1 问题分析
给定两个序列X={x1,x2,x3,…,xm}和Y={y1,y2,y3,…,yn},找出X和Y的一个最长的公共子序列。
例如:X=(A,B,C,B,A,D,B),Y=(B,C,B,A,A,C),那么最长公共子序列是B,C,B,A。
如何找到最长公共子序列呢?
如果使用暴力搜索方法,需要穷举X的所有子序列,检查每个子序列是否也是Y的子序列,记录找到的最长公共子序列。X的子序列有2m个,因此暴力求解的方法时间复杂度为指数阶,这是我们避之不及的爆炸性时间复杂度。
那么能不能用动态规划算法呢?
下面分析该问题是否具有最优子结构性质。
(1)分析最优解的结构特征
假设已经知道Zk={z1,z2,z3,…,zk}是Xm={x1,x2,x3,…,xm}和Yn={y1,y2,y3,…,yn}的最长公共子序列。这个假设很重要,我们都是这样假设已经知道了最优解。
那么可以分3种情况讨论。
- xm= yn= zk:那么Zk−1={z1,z2,z3,…,zk−1}是Xm−1和Yn−1的最长公共子序列,如图4-4所示。
反证法证明 : 如果Zk−1={z1,z2,z3,…,zk−1}不是Xm−1和Yn−1的最长公共子序列,那么它们一定存在一个最长公共子序列。设M为Xm−1和Yn−1的最长公共子序列,M的长度大于Zk−1的长度,即|M|>|Zk−1|。如果在Xm−1和Yn−1的后面添加一个相同的字符xm= yn,则zk=xm=yn,|M+{zk}|>|Zk−1+{zk}|=|Zk|,那么Zk不是Xm和Yn的最长公共子序列,这与假设Zk是Xm和Yn的最长公共子序列矛盾,问题得证。
- xm≠yn,xm≠ zk:我们可以把xm去掉,那么Zk是Xm−1和Yn的最长公共子序列,如图4-5所示。
反证法证明: 如果Zk不是Xm−1和Yn的最长公共子序列,那么它们一定存在一个最长公共子序列。设M为Xm−1和Yn的最长公共子序列,M的长度大于Zk的长度,即|M|>|Zk|。如果我们在Xm−1的后面添加一个字符xm,那么M也是Xm和Yn的最长公共子序列,因为|M|>|Zk|,那么Zk不是Xm和Yn的最长公共子序列,这与假设Zk是Xm和Yn的最长公共子序列矛盾,问题得证。
- xm≠yn,yn≠ zk:我们可以把yn去掉,那么Zk是Xm和Yn−1的最长公共子序列,如图4-6所示。
反证法证明: 如果Zk不是Xm和Yn−1的最长公共子序列,那么它们一定存在一个最长公共子序列。设M为Xm和Yn−1的最长公共子序列,M的长度大于Zk的长度,即|M|>|Zk|。如果我们在Yn−1的后面添加一个字符yn,那么M也是Xm和Yn的最长公共子序列,因为|M|>|Zk|,那么Zk不是Xm和Yn的最长公共子序列,这与假设Zk是Xm和Yn的最长公共子序列矛盾,问题得证。
(2)建立最优值的递归式。
设c[i][j]表示Xi和Yj的最长公共子序列长度。
- xm= yn= zk:那么c[i][j]= c[i−1][j−1]+1;
- xm≠yn:那么我们只需要求解Xi和Yj−1的最长公共子序列和Xi−1和Yj的最长公共子序列,比较它们的长度哪一个更大,就取哪一个值。即c[i][j]= max{c[i][j−1], c[i−1][j]}。
- 最长公共子序列长度递归式:
(3)底向上计算最优值,并记录最优值和最优策略
i=1时:{x1}和{y1,y2,y3,…,yn}中的字符一一比较,按递归式求解并记录最长公共子序列长度。
i=2时:{x2}和{y1,y2,y3,…,yn}中的字符一一比较,按递归式求解并记录最长公共子序列长度。
……
i=m时:{xm}和{y1,y2,y3,…,yn}中的字符一一比较,按递归式求解并记录最长公共子序列长度。
(4)构造最优解
上面的求解过程只是得到了最长公共子序列长度,并不知道最长公共子序列是什么,那怎么办呢?
例如,现在已经求出c[m][n]=5,表示Xm和Yn的最长公共子序列长度是5,那么这个5是怎么得到的呢?我们可以反向追踪5是从哪里来的。根据递推式,有如下情况。
xi= yj时:c[i][j]= c[i−1][j−1]+1;
xi≠yj时:c[i][j]= max{c[i][j−1], c[i−1][j]};
那么c[i][j]的来源一共有3个:c[i][j]= c[i−1][j−1]+1,c[i][j]= c[i][j−1],c[i][j]= c[i−1][j]。在第3步自底向上计算最优值时,用一个辅助数组b [i][j]记录这3个来源:
c[i][j]= c[i−1][j−1]+1,b[i][j]=1;
c[i][j]= c[i][j−1],b[i][j]=2;
c[i][j]= c[i−1][j],b[i][j]=3。
这样就可以根据b[m][n]反向追踪最长公共子序列,当b[i][j]=1时,输出xi;当b [i][j]=2时,追踪c[i][j−1];当b[i][j]=3时,追踪c[i−1][j],直到i=0或j=0停止。
4.3.2 算法设计
最长公共子序列问题满足动态规划的最优子结构性质,可以自底向上逐步得到最优解。
(1)确定合适的数据结构
采用二维数组c[][]来记录最长公共子序列的长度,二维数组b[][]来记录最长公共子序列的长度的来源,以便算法结束时倒推求解得到该最长公共子序列。
(2)初始化
输入两个字符串s1、s2,初始化c[][]第一行第一列元素为0。
(3)循环阶段
- i = 1:s1[0]与s2[j−1]比较,j=1,2,3,…,len2。
如果s1[0]=s2[j−1],c[i][j] = c[i−1][j−1]+1;并记录最优策略来源b[i][j]=1;
如果s1[0] ≠s2[j−1],则公共子序列的长度为c[i][j−1]和c[i−1][j]中的最大值,如果c[i][j−1]≥c[i−1][j],则c[i][j]=c[i][j−1],最优策略来源b[i][j]=2;否则c[i][j]= c[i−1][j],最优策略来源b[i][j]=3。
- i = 2:s1[1]与s2[j−1]比较,j=1,2,3,…,len2。
- 以此类推,直到i > len1时,算法结束,这时c[len1][len2]就是最长公共序列的长度。
(4)构造最优解
根据最优决策信息数组b[][]递归构造最优解,即输出最长公共子序列。因为我们在求最长公共子序列长度c[i][j]的过程中,用b[i][j]记录了c[i][j]的来源,那么就可以根据b[i][j]数组倒推最优解。
如果b[i][j]=1,说明s1[i−1]=s2[j−1],那么就可以递归求解print(i−1, j−1);然后输出s1[i−1]。
注意: 如果先输出,后递归求解print(i−1,j−1),则输出的结果是倒序。
如果b[i][j]=2,说明s1[i−1]≠s2[j−1]且最优解来源于c[i][j]=c[i][j−1],递归求解print(i, j−1)。
如果b[i][j]=3,说明s1[i−1]≠s2[j−1]且最优解来源于c[i][j]=c[i−1][j],递归求解print(i−1, j)。当i==0 || j==0时,递归结束。
4.3.3 完美图解
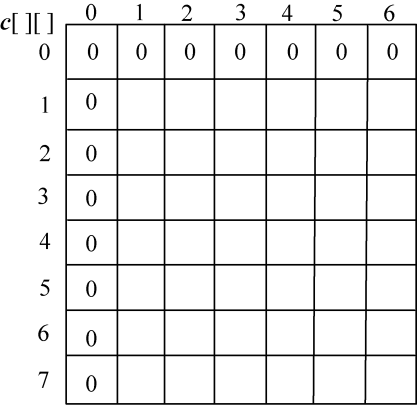
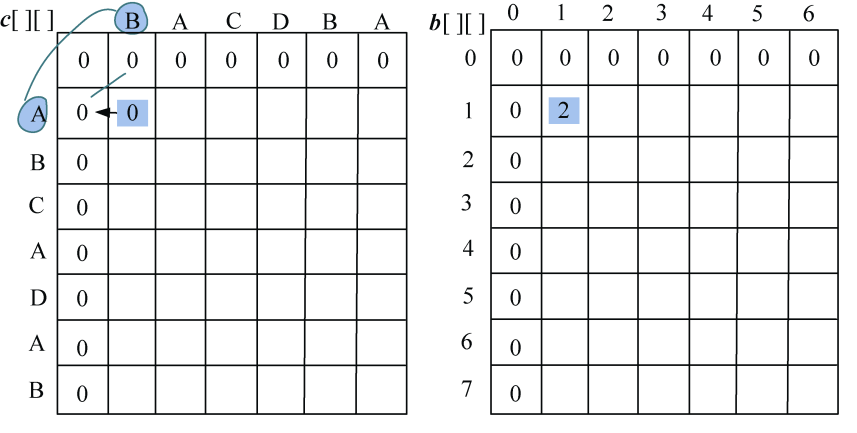
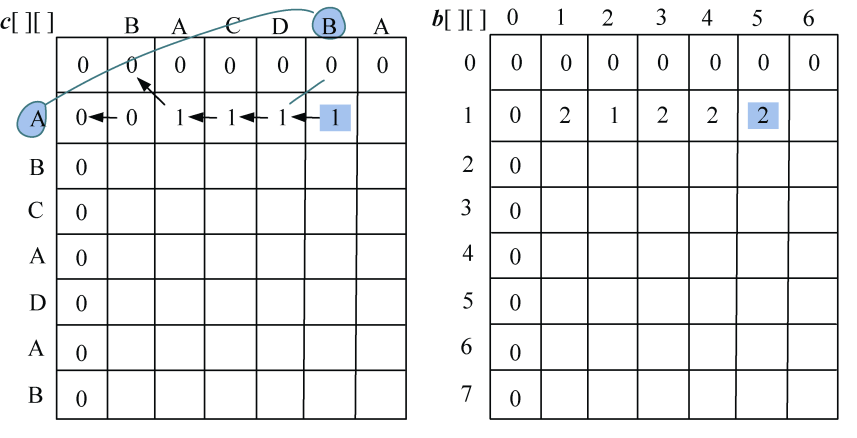
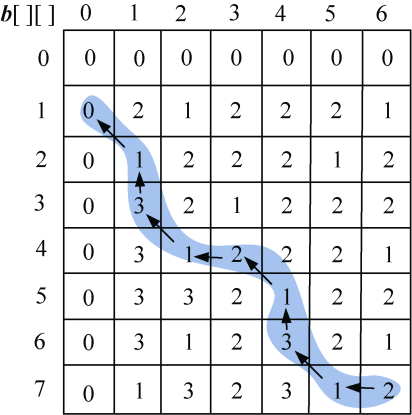
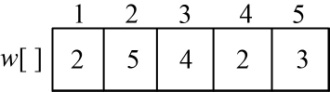
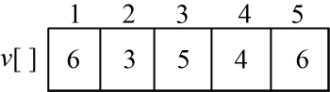
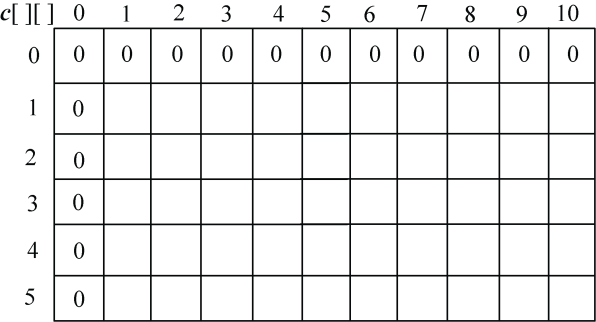
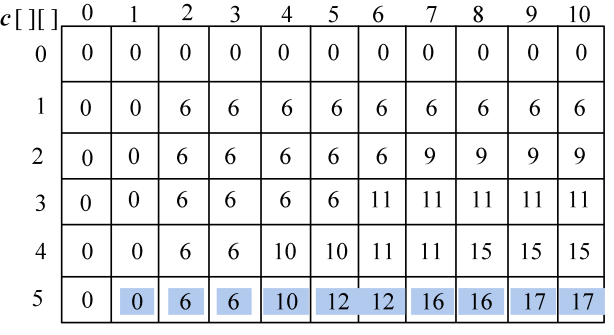
以字符串s1=“ABCADAB”,s2=“BACDBA”为例。
(1)初始化
len1=7,len2=6,初始化c[][]第一行、第一列元素为0,如图4-7所示。
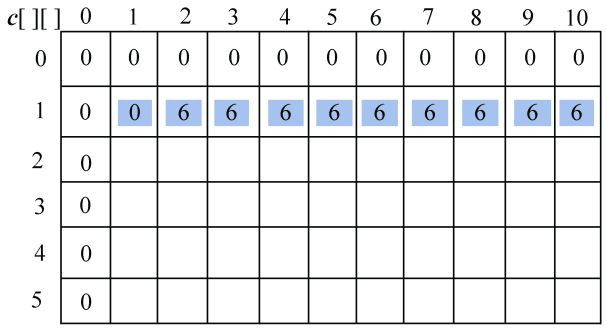
(2)i=1:s1[0]与s2[j−1]比较,j=1,2,3,…,len2。即“A”与“BACDBA”分别比较一次。
如果字符相等,c[i][j]取左上角数值加1,记录最优值来源b[i][j]=1。
如果字符不等,取左侧和上面数值中的最大值。如果左侧和上面数值相等,默认取左侧数值。如果c[i][j]的值来源于左侧b[i][j]=2,来源于上面b[i][j]=3。
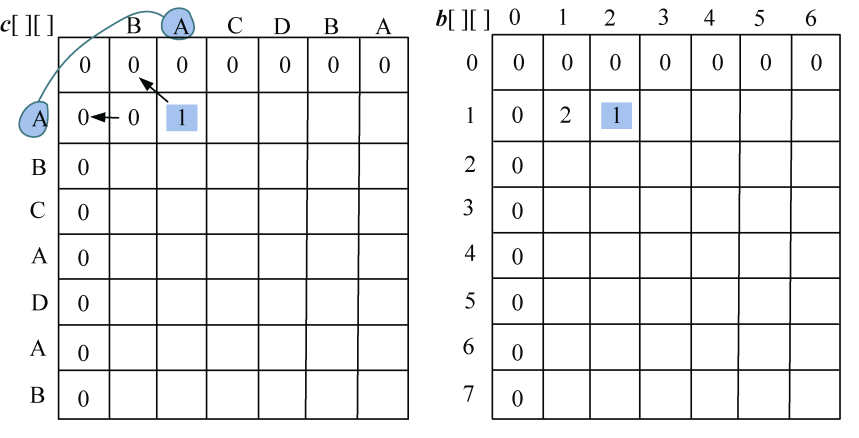
- j=1:A≠B,左侧=上面,取左侧数值,c[1][1]= 0,最优策略来源b[1][1]=2,如图4-8所示。
- j=2:A=A,则取左上角数值加1,c[1][2]= c[0][1]+1=2,最优策略来源b[1][2] =1,如图4-9所示。
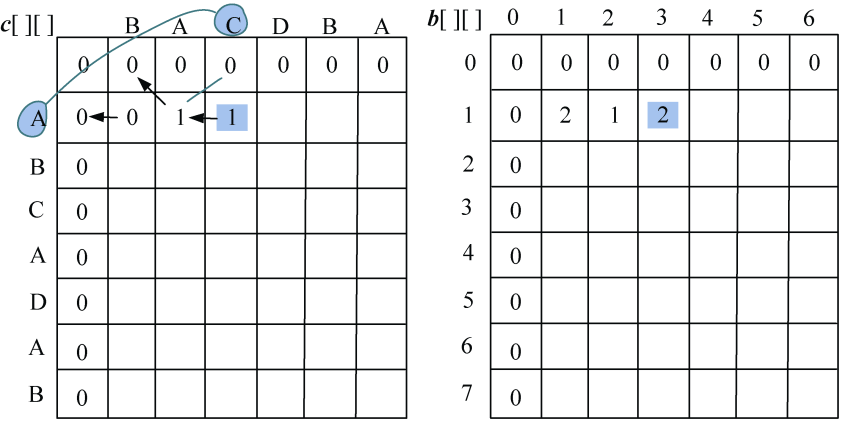
- j=3:A≠C,左侧≥上面,取左侧数值,c[1][3]= 1,最优策略来源b[1][3] =2,如图4-10所示。
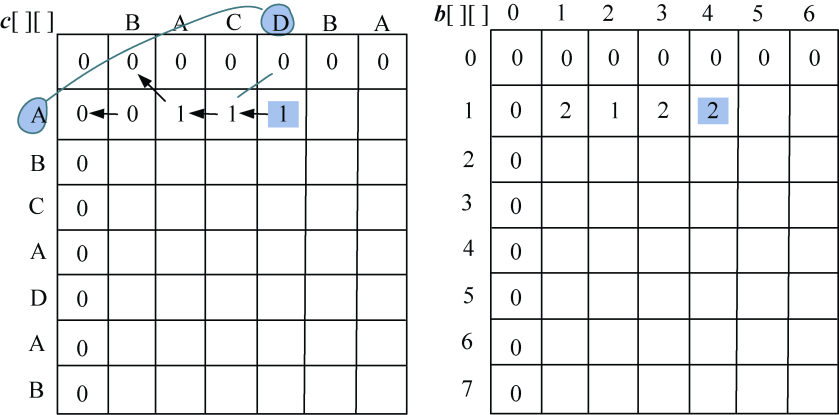
- j= 4:A≠D,左侧≥上面,取左侧数值,c[1][4]= 1,最优策略来源b[1][4] =2,如图4-11所示。
- j=5:A≠B,左侧≥上面,取左侧数值,c[1][5]=1,最优策略来源b[1][5]=2,如图4-12所示。
- j=6:A=A,则取左上角数值加1,c[1][6]=1,最优策略来源b[1][6]=1,如图4-13所示。
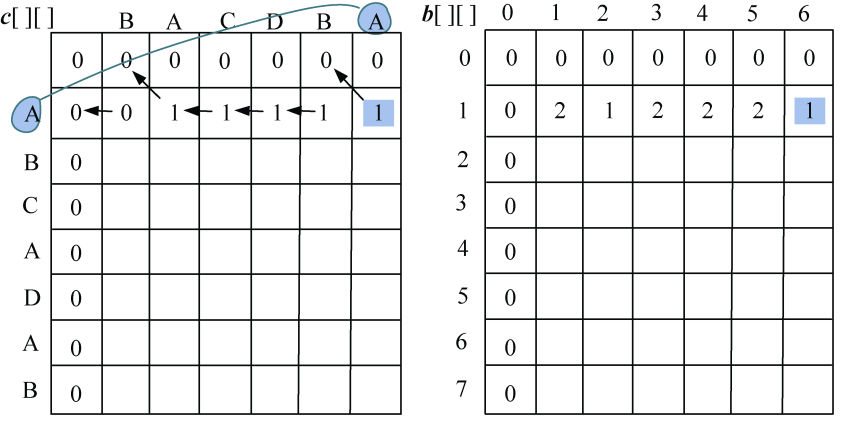
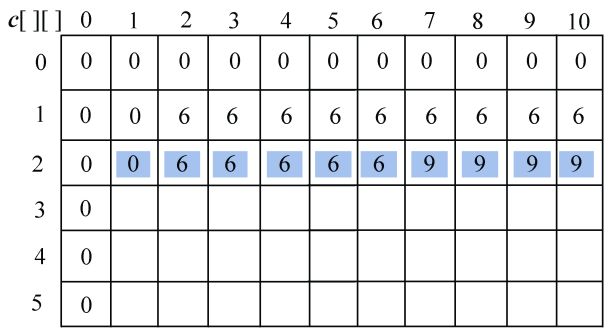
(3)i=2:s1[1]与s2[j−1]比较,j=1,2,3,…,len2。即“B”与“BACDBA”分别比较一次。
如果字符相等,c[i][j]取左上角数值加1,记录最优值来源b[i][j]=1。
如果字符不等,取左侧和上面数值中的最大值。如果左侧和上面数值相等,默认取左侧数值。如果c[i][j]的值来源于左侧b[i][j]=2,来源于上面b[i][j]=3,如图4-14所示。
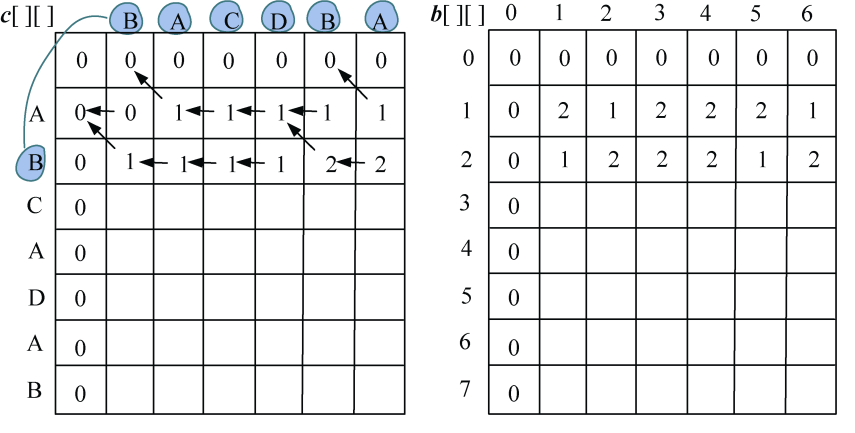
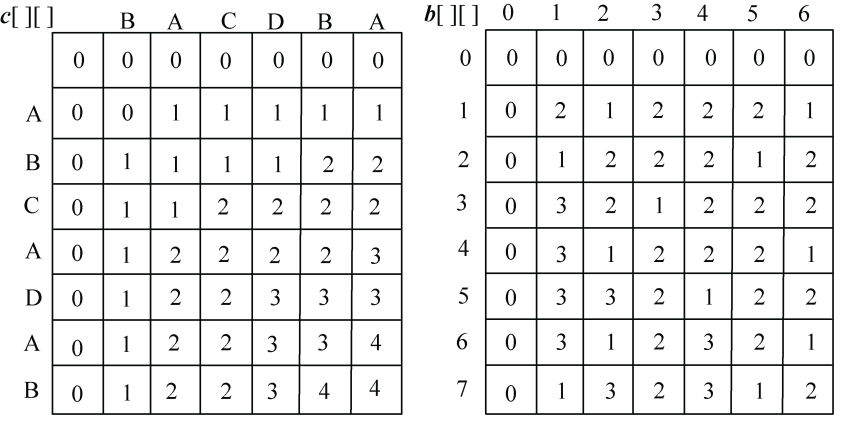
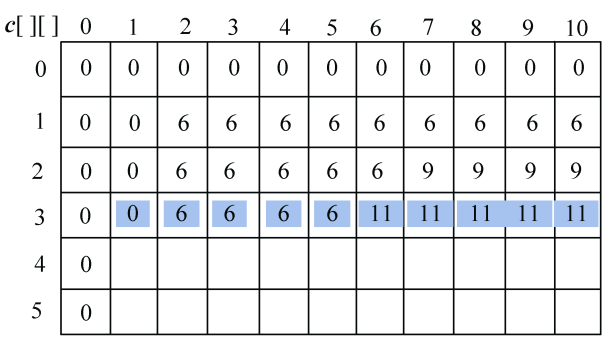
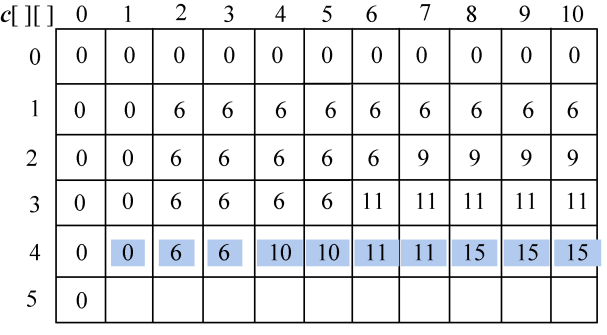
(4)继续处理i=2,3,…,len1:s1[i−1]与s2[j−1]比较,j=1,2,3,…,len2。处理结果如图4-15所示。
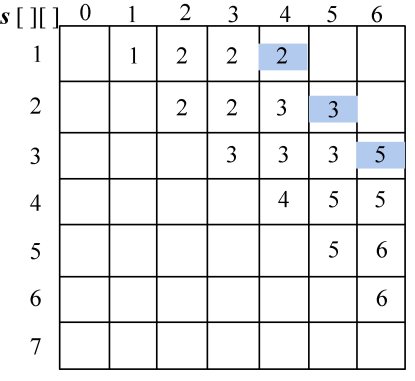
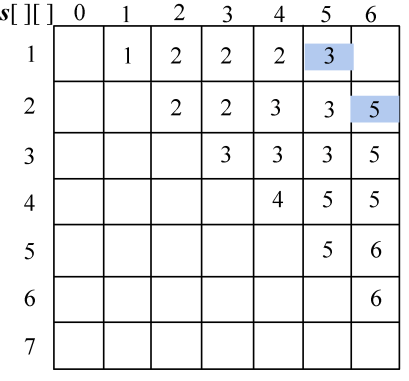
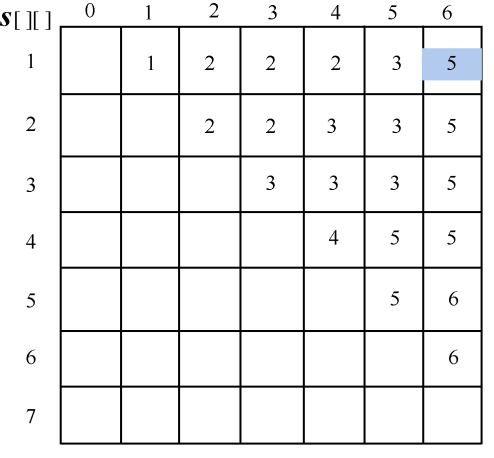
c[][]右下角的值即为最长公共子序列的长度。c[7][6]=4,即字符串s1=“ABCADAB”,s2=“BACDBA”的最长公共子序列的长度为4。
那么最长公共子序列包含哪些字符呢?
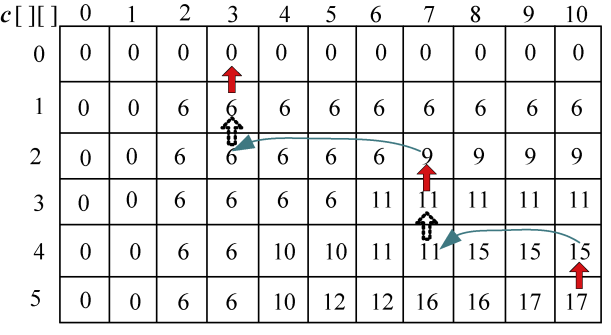
(5)构造最优解
首先读取b[7][6]=2,说明来源为2,向左找b[7][5];
b[7][5]=1,向左上角找b[6][4],返回时输出s[6]=“B”;
b[6][4]=3,向上找b[5][4];
b[5][4]=1,向左上角找b[4][3],返回时输出s[4]=“D”;
b[4][3]=2,向左找b[4][2];
b[4][2]=1,向左上角找b[3][1],返回时输出s[3]=“C”;
b[3][1]=3,向上找b[2][1];
b[2][1]=1,向左上角找,返回时输出s[1]=“B”;
b[1][0]中列为0,算法停止,返回,输出最长公共子序列为BCDB,如图4-16所示。
4.3.4 伪代码详解
(1)最长公共子序列求解函数
首先计算两个字符串的长度,然后从i=1开始,s1[0]与s2中的每一个字符比较。
如果当前字符相同,则公共子序列的长度为c[i−1][j−1]+1,并记录最优策略来源b[i][j] = 1。
如果当前字符不相同,则公共子序列的长度为c[i][j−1]和c[i−1][j]中的最大值,如果c[i][j−1]≥c[i−1][j],则最优策略来源b[i][j]=2;如果c[i][j−1]<c[i−1][j],则最优策略来源b[i][j]=3。直到i> len1时,算法结束,这时c[len1][len2]就是我们要的最长公共序列长度。
1 | Void LCSL() |
(2)最优解输出函数
输出最优解仍然使用倒推法。因为我们在求最长公共子序列长度c[i][j]的过程中,用b[i][j]记录了c[i][j]的来源,那么就可以根据b[i][j]数组倒推最优解。
如果b[i][j]=1,说明s1[i−1]=s2[j−1],那么我们就可以递归输出print(i−1,j−1);然后输出s1[i−1]。
如果b[i][j]=2,说明s1[i−1]≠s2[j−1]且最优解来源于c[i][j]=c[i][j−1],递归输出print(i,j−1)。
如果b[i][j]=3,说明s1[i−1]≠s2[j−1]且最优解来源于c[i][j]=c[i−1][j],递归输出print(i−1,j)。当i==0||j==0时,递归结束。
1 | Void print(int I, int j)//根据记录下来的信息构造最长公共子序列(从b[i][j]开始递推) |
4.3.5 实战演练
1 | //program 4-1 |
算法实现和测试
(1)运行环境
Code::Blocks
(2)输入
1 | 输入字符串s1: |
(3)输出
1 | s1和s2的最长公共子序列长度是:4 |
4.3.6 算法解析及优化拓展
1.算法复杂度分析
(1)时间复杂度:由于每个数组单元的计算耗费Ο(1)时间,如果两个字符串的长度分别是m、n,那么算法时间复杂度为Ο(m*n)。
(2)空间复杂度:空间复杂度主要为两个二维数组c[][],b[][],占用的空间为O(m*n)。
2.算法优化拓展
因为c[i][j]有3种来源:c[i−1][j−1]+1、c[i][j−1]、c[i−1][j]。我们可以利用c数组本身来判断来源于哪个值,从而不用b[][],这样可以节省O(mn)个空间。但因为c数组还是O(mn)个空间,所有空间复杂度数量级仍然是O(m*n),只是从常数因子上的改进。仍然是倒推的办法,如图4-17所示,读者可以想一想怎么做?
4.4 DNA基因鉴定——编辑距离
我们经常会听说DNA亲子鉴定是怎么回事呢?人类的DNA由4个基本字母{A,C,G,T}构成,包含了多达30亿个字符。如果两个人的DNA序列相差0.1%,仍然意味着有300万个位置不同,所以我们通常看到的DNA亲子鉴定报告上结论有:相似度99.99%,不排除亲子关系。
怎么判断两个基因的相似度呢?生物学上给出了一种编辑距离的概念。
例如两个字符串FAMILY和FRAME,有两种对齐方式:
F - A M I L Y - F A M I L Y
F R A M E F R A M E
第1种对齐需要付出的代价:4,插入R,将I替换为E,删除L、Y。
第2种对齐需要付出的代价:5,插入R,将F替换为R,将I替换为E,删除L、Y。
编辑距离是指将一个字符串变换为另一个字符串所需要的最小编辑操作。
怎么找到两个字符串x[1,…,m]和y[1,…,n]的编辑距离呢?
4.4.1 问题分析
编辑距离是指将一个字符串变换为另一个字符串所需要的最小编辑操作。
给定两个序列X={x1,x2,x3,…,xm}和Y={y1,y2,y3,…,yn},找出X和Y的编辑距离。
例如:X=(A,B,C,D,A,B),Y=(B,D,C,A,B)。如果用穷举法,会有很多种对齐方式,暴力穷举的方法是不可取的。那么怎么找到编辑距离呢?
首先考虑能不能把原问题变成规模更小的子问题,如果可以,那就会容易得多。
要求两个字符串X={x1,x2,x3,…,xm}和Y={y1,y2,y3,…,yn}的编辑距离,那么可以求其前缀Xi={x1,x2,x3,…,xi}和Yj={y1,y2,y3,…,yj}的编辑距离,当i=m,j=n时就得到了所有字符的编辑距离。
那么能不能用动态规划算法呢?
下面我们分析该问题是否具有最优子结构性质。
(1)分析最优解的结构特征
假设已经知道d[i][j]是Xi={x1,x2,x3,…,xi}和Yj={y1,y2,y3,…,yj}的编辑距离最优解。这个假设很重要,我们都是这样假设已经知道了最优解。
那么两个序列无论怎么对齐,其右侧只可能有如下3种对齐方式:
- 如图4-19所示。需要删除xi,付出代价1,那么我们只需要求解子问题{x1,x2,x3,…,xi−1}和{y1,y2,y3,…,yj}的编辑距离再加1即可,即d[i][j]=d[i−1][j]+1。d[i−1][j]是Xi−1和Yj的最优解。
反证法证明: 设d[i−1][j]不是Xi−1和Yj的最优解,那么它们一定存在一个最优解d’,d’<d[i−1][j]。如果在Xi−1的后面添加一个字符xi,d’+1也是Xi和Yj的最优解,因为d’+1<d[i−1][j]+1=d[i][j],所以d[i][j]不是Xi和Yj的最优解,这与假设d[i][j]是Xi和Yj的最优解矛盾,问题得证。
- 如图4-20所示。需要插入yj,付出代价1,那么我们只需要求解子问题{x1,x2,x3,…,xi}和{y1,y2,y3,…,yj−1}的编辑距离再加1即可,即d[i][j]=d[i][j−1]+1。d[i][j−1]是Xi和Yj−1的最优解。
同理可证。
- 如图4-21所示。如果xi=yj,付出代价0,如果xi≠yj,需要替换,付出代价1,我们用函数diff(i,j)来表达,xi=yj时,diff(i,j)=0;xi≠yj时,diff(i,j)=1。那么我们只需要求解子问题{x1,x2,x3,…,xi−1}和{y1,y2,y3,…,yj−1}的编辑距离再加diff(i,j)即可,即d[i][j]=d[i−1][j−1]+ diff(i,j)。d[i−1][j−1]是Xi−1和Yj−1的最优解。
同理可证。
(2)建立最优值递归式
设d[i][j]表示Xi和Yj的编辑距离,则d[i][j]取以上三者对齐方式的最小值。
编辑距离递归式:
(3)自底向上计算最优值,并记录最优值和最优策略
i=1时:{x1}和{y1,y2,y3,…,yn}中的字符一一比较,按递归式求解并记录编辑距离。
i=2时:{x2}和{y1,y2,y3,…,yn}中的字符一一比较,按递归式求解并记录编辑距离。
……
i=m时:{xm}和{y1,y2,y3,…,yn}中的字符一一比较,按递归式求解并记录编辑距离。
(4)构造最优解
如果仅仅需要知道编辑距离是多少,上面的求解过程得到的编辑距离就是最优值。如果还想知道插入、删除、替换了哪些字母,就需要从d[i][j]表格中倒推,输出这些结果。
4.4.2 算法设计
编辑距离问题满足动态规划的最优子结构性质,可以自底向上逐渐推出整体最优解。
(1)确定合适的数据结构
采用二维数组d[][]来记录编辑距离。
(2)初始化
输入两个字符串s1、s2,初始化d[][]第一行为0,1,2,…,len2,第一列元素为0,1,2,…,len1。
(3)循环阶段
- i=1:s1[0]与s2[j−1]比较,j=1,2,3,…,len2。
如果s1[0]=s2[j−1],diff[i][j] = 0。
如果s1[0] ≠s2[j−1],则diff[i][j] =1。
- i=2:s1[1]与s2[j−1]比较,j=1,2,3,…,len2。
- 以此类推,直到i >len1时,算法结束,这时d[len1][len2]就是我们要的最优解。
(4)构造最优解
从d[i][j]表格中倒推,输出插入、删除、替换了哪些字母。在此没有使用辅助数组,采用判断的方式倒推。
4.4.3 完美图解
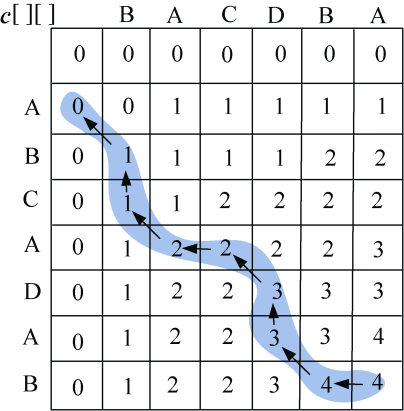
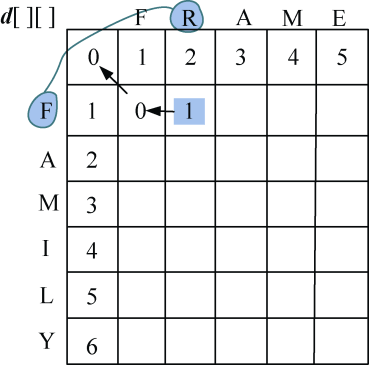
以字符串s1=” FAMILY”,s2=” FRAME”为例。
(1)初始化
len1=6,len2=5,初始化d[][]第一行为0,1,2,…,5,第一列元素为0,1,2,…,6,如图4-22所示。
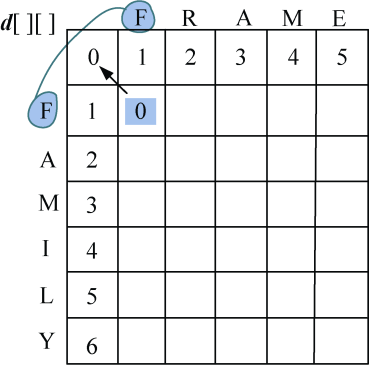
(2)i=1:s1[0]与s2[j−1]比较,j=1,2,3,…,len2。即“F”与“FRAME”分别比较一次。
如果字符相等,diff[i][j]=0,否则diff[i][j] = 1。按照递归公式:
即取上面+1,左侧+1,左上角数值加diff[i][j]3个数当中的最小值,相等时取后者。
- j=1:F=F,diff[1][1]=0,左上角数值加diff[1][1]=0,左侧+1=上面+1=2,3个数当中的最小值,d[1][1] =0,如图4-23所示。
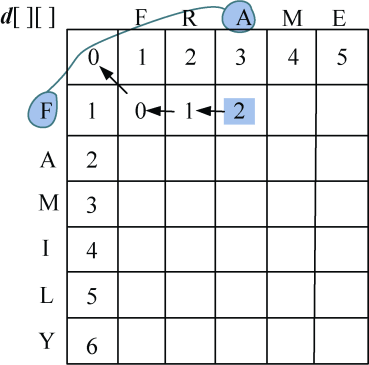
- j=2:F≠R,diff[1][2]=1,左上角数值加diff[1][2]=2,左侧+1=1,上面+1=3,取3个数当中的最小值,d[1][2] =1,如图4-24所示。
- j=3:F≠A,diff[1][3]=1,左上角数值加diff[1][3]=3,左侧+1=2,上面+1=4,取3个数当中的最小值,d[1][3] =2,如图4-25所示。
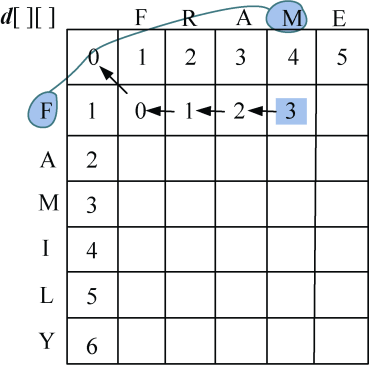
- j=4:F≠M:diff[1][4]=1,左上角数值加diff[1][4]=4,左侧+1=3,上面+1=5,取3个数当中的最小值,d[1][4] =3,如图4-26所示。
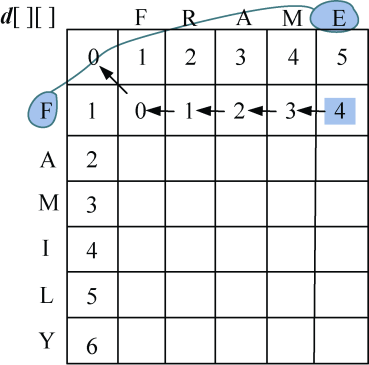
- j=5:F≠E,diff[1][5]=1,左上角数值加diff[1][5]=5,左侧+1=4,上面+1=6,取3个数当中的最小值,d[1][5] =4,如图4-27所示。
(3)i=2:s1[1]与s2[j−1]比较,j=1,2,3,…,len2。即“A”与“FRAME”分别比较一次。
如果字符相等,diff[i][j]=0,否则diff[i][j] = 1。按照递归公式:
即取上面+1,左侧+1,左上角数值加diff[i][j]3个数当中的最小值,相等时取后者。
填写完毕,如图4-28所示。
(4)继续处理i=2,3,…,len1:s1[i−1]与s2[j−1]比较,j=1,2,3,…,len2,处理结果如图4-29所示。
(5)构造最优解
从右下角开始,逆向查找d[i][j]的来源: 上面 (即d[i][j]=d[i−1][j]+1)表示需要删除, 左侧 (即d[i][j]=d[i][j−1]+1)表示需要插入, 左上角 (即d[i][j]=d[i−1][j−1]+diff[i][j])要判断是否字符相等,如果不相等则需要替换,如果字符相等什么也不做,如图4-30所示。为什么是这样呢?不清楚的读者可以回看4.4.1节。
- 首先读取右下角d[6][5]=4,s1[5]≠s2[4],d[6][5]来源于3个数当中的最小值:上面+1=4,左侧+1=5,左上角数值+diff[i][j]=4,相等时取后者。来源于左上角,需要替换操作。返回时输出s1[5]替换为s2[4],即“Y” 替换 为“E”。
- 向左上角找d[5][4]=3,s1[4]≠s2[3]。d[5][4]来源于3个数当中的最小值:上面+1=3,左侧+1=5,左上角数值+diff[i][j]=4。来源于上面,需要删除操作。返回时输出删除s1[4],即 删除 “L”。
- 向上面找d[4][4]=2,s1[3]≠s2[3]。d[4][4]来源于3个数当中的最小值:上面+1=2,左侧+1=4,左上角数值+diff[i][j]=3。来源于上面,需要删除操作。返回时输出删除s1[3],即 删除 “I”。
- 向上面找d[3][4]=1,s1[2]=s2[3],不需操作。d[3][4]来源于上面+1=3,左侧+1=3,左上角数值+diff[i][j]=13个数当中的最小值。来源于左上角,因为字符相等什么也不做。返回时不输出。
- 向左上角找d[2][3]=1,s1[1]=s2[2],不需操作。d[2][3]来源于3个数当中的最小值:上面+1=3,左侧+1=2,左上角数值+diff[i][j]=1。来源于左上角,因为字符相等什么也不做。返回时不输出。
- 向左上角找d[1][2]=1,s1[0]≠s2[1]。d[1][2]来源于3个数当中的最小值:上面+1=3,左侧+1=1,左上角数值+diff[i][j]=2。来源于左则,需要插入操作。返回时输出在第1个字符之后插入s2[1],即 插入 “R”。
- 向左则找d[1][1]=0,s1[0]=s2[0]。d[1][1]来源于3个数当中的最小值:上面+1=2,左侧+1=2,左上角数值+diff[i][j]=0。来源于左上角,因为字符相等什么也不做。返回时不输出。
- 行或列为0时,算法停止。
4.4.4 伪代码详解
编辑距离求解函数:首先计算两个字符串的长度,然后从i=1开始,比较s1[0]和s2[]中的每一个字符,如果字符相等,diff[i][j]=0,否则diff[i][j]=1。因为这个值不需要记录,仅在公式表达时用数组表示,在程序设计时只用一个变量diff就可以了。
取上面+1(即d[i][j]=d[i−1][j]+1),左侧+1(即d[i][j]=d[i][j−1]+1),左上角数值+diff[i][j] (即d[i][j]=d[i−1][j−1]+ diff[i][j])三者当中的最小值,相等时取后者。
直到i>len1时,算法结束,这时d[len1][len2]就是我们要的编辑距离。
1 | int editdistance(char *str1, char *str2) |
4.4.5 实战演练
1 | //program 4-2 |
算法实现和测试
(1)运行环境
Code::Blocks
(2)输入
1 | 输入字符串str1: |
(3)输出
1 | family和frame的编辑距离是:4 |
4.4.6 算法解析及优化拓展
1.算法复杂度分析
(1)时间复杂度:算法有两个for循环,一个双重for循环。如果两个字符串的长度分别是m、n,前两个for循环时间复杂度为O(n)和O(m),双重for循环时间复杂度为O(nm),所以总的时间复杂度为O(nm)。
(2)空间复杂度:使用了d[][]数组,空间复杂度为O(n*m)。
2.算法优化拓展
大家可以动手实现构造最优解部分,可以直接倒推,也可以在程序开始使用辅助数组记录来源,然后倒推。
想一想还有没有更好的算法求解呢?
4.5 长江一日游——游艇租赁
长江游艇俱乐部在长江上设置了n个游艇出租站,游客可以在这些游艇出租站租用游艇,并在下游的任何一个游艇出租站归还游艇。游艇出租站i到游艇出租站j之间的租金为r(i,j),1≤i<j≤n。试设计一个算法,计算从游艇出租站i到出租站j所需的最少租金。
4.5.1 问题分析
长江游艇俱乐部在长江上设置了n个游艇出租站,游客可以在这些出租站租用游艇,并在下游的任何一个游艇出租站归还游艇。游艇出租站i到游艇出租站j之间的租金为r(i,j)。现在要求出从游艇出租站1到游艇出租站n所需的最少的租金。
当要租用游艇从一个站到另外一个站时,中间可能经过很多站点,不同的停靠站策略就有不同的租金。那么我们可以考虑该问题,从第1站到第n站的最优解是否一定包含前n−1的最优解,即是否具有最优子结构和重叠性。如果是,就可以利用动态规划进行求解。
如果我们穷举所有的停靠策略,例如一共有10个站点,当求子问题4个站点的停靠策略时,子问题有(1,2,3,4),(2,3,4,5),(3,4,5,6),(4,5,6,7),(5,6,7,8),(6,7,8,9),(7,8,9,10)。如果再求其子问题3个站点的停靠策略,(1,2,3,4)产生两个子问题:(1,2,3),(2,3,4)。(2,3,4,5)产生两个子问题:(2,3,4),(3,4,5)。如果再继续求解子问题,会发现有大量的子问题重叠,其算法时间复杂度为2n,暴力穷举的办法是很不可取的。
下面分析第i个站点到第j个站点(i,i+1,…,j)的最优解(最少租金)问题,考查是否具有最优子结构性质。
(1)分析最优解的结构特征
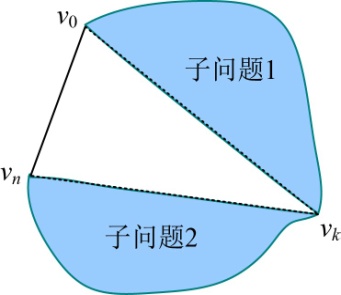
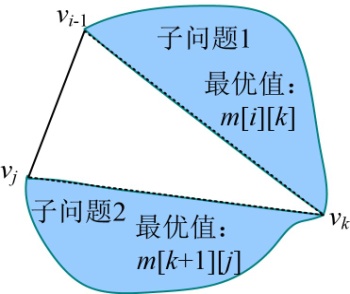
- 假设我们已经知道了在第k个站点停靠会得到最优解,那么原问题就变成了两个子问题:(i,i+1,…,k)、(k,k+1,…,j)。如图4-32所示。
- 那么原问题的最优解是否包含子问题的最优解呢?
假设第i个站点到第j个站点(i,i+1,…,j)的最优解是c,子问题(i,i+1,…,k)的最优解是a,子问题(k,k+1,…,j)的最优解是b,那么c=a+b,无论两个子问题的停靠策略如何都不影响它们的结果,因此我们只需要证明如果c是最优的,则a和b一定是最优的(即原问题的最优解包含子问题的最优解)。
反证法 :如果a不是最优的,子问题(i,i+1,…,k)存在一个最优解a’,a’<a,那么a’+b <c,所以c不是最优的,这与假设c是最优的矛盾,因此如果c是最优的,则a一定是最优的。同理可证b也是最优的。因此如果c是最优的,则a和b一定是最优的。
因此,该问题具有最优子结构性质。
(2)建立最优值的递归式
- 用m[i][j]表示第i个站点到第j个站点(i,i+1,…,j)的最优值(最少租金),那么两个子问题:(i,i+1,…,k)、(k,k+1,…,j)对应的最优值分别是m[i][k]、m[k][j]。
- 游艇租金最优值递归式:
当j=i时,只有1个站点,m[i][j]=0。
当j=i+1时,只有2个站点,m[i][j]= r[i][j]。
当j>i+1时,有3个以上站点,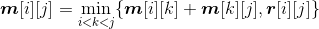
整理如下。
(3)自底向上计算最优值,并记录
先求两个站点之间的最优值,再求3个站点之间的最优值,直到n个站点之间的最优值。
(4)构造最优解
上面得到的最优值只是第1个站点到第n个站点之间的最少租金,并不知道停靠了哪些站点,我们需要从记录表中还原,逆向构造出最优解。
4.5.2 算法设计
采用自底向上的方法求最优值,分为不同规模的子问题,对于每一个小的子问题都求最优值,记录最优策略,具体策略如下。
(1)确定合适的数据结构
采用二维数组r[][]输入数据,二维数组m[][]存放各个子问题的最优值,二维数组s[][]存放各个子问题的最优决策(停靠站点)。
(2)初始化
根据递推公式,可以把m[i][j]初始化为r[i][j],然后再找有没有比m[i][j]小的值,如果有,则记录该最优值和最优解即可。初始化为:m[i][j]=r[i][j],s[i][j]=0,其中,i=1,2,…,n,j=i+1,i+2,…,n。
(3)循环阶段
- 按照递归关系式计算3个站点i,i+1,j(j=i+2)的最优值,并将其存入m[i][j],同时将最优策略记入s[i][j],i=1,2,…,n−2。
- 按照递归关系式计算4个站点i,i+1,i+2,j(j=i+3)的最优值,并将其存入m[i][j],同时将最优策略记入s[i][j],i=1,2,…,n−3。
- 以此类推,直到求出n个站点的最优值m[1][n]。
(4)构造最优解
根据最优决策信息数组s[][]递归构造最优解。s[1][n]是第1个站点到第n个站点(1,2,…,n)的最优解的停靠站点,即停靠了第s[1][n]个站点,我们在递归构造两个子问题(1,2,…,k)和(k,k +1,…,n)的最优解停靠站点,一直递归到子问题只包含一个站点为止。
4.5.3 完美图解
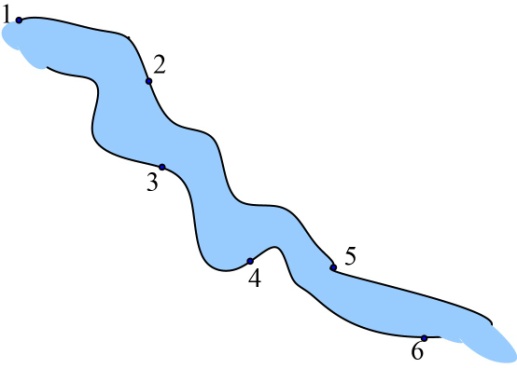
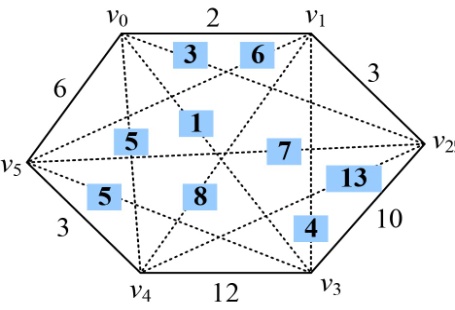
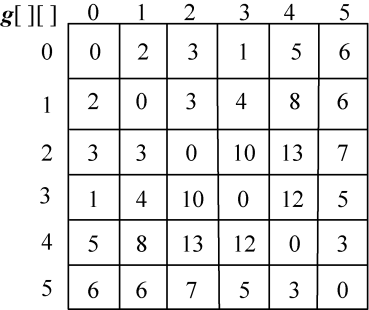
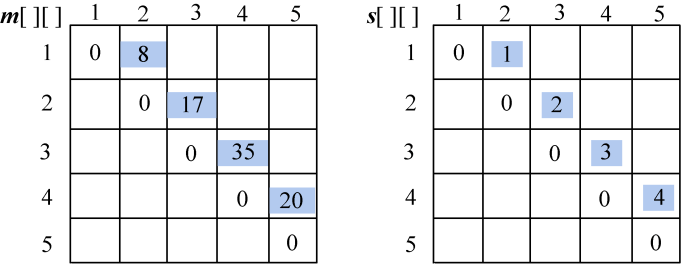
长江游艇俱乐部在长江上设置了6个游艇出租站,如图4-33所示。游客可以在这些出租站租用游艇,并在下游的任何一个游艇出租站归还游艇。游艇出租站i到游艇出租站j之间的租金为r(i,j),如图4-34所示。
(1)初始化
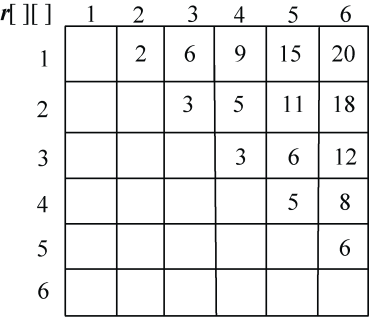
节点数n=6,m[i][j]=r[i][j],s[i][j]=0,其中,i=1,2,…,n,j=i+1,i+2,…,n。如图4-35所示。
(2)计算3个站点i,i+1,j(j=i+2)的最优值,并将其存入m[i][j],同时将最优策略记入s[i][j],i=1,2,3,4。
- i = 1,j=3:m[1][2]+ m[2][3]=5 < m[1][3]=6,更新m[1][3]=5,s[1][3]=2。
- i = 2,j=4:m[2][3]+ m[3][4]=6 > m[2][4]=5,不做改变。
- i = 3,j=5:m[3][4]+ m[4][5] =7> m[3][5]=6,不做改变。
- i = 4,j=6:m[4][5]+ m[5][6]=9 > m[4][6]=8,不做改变。
如图4-36所示。
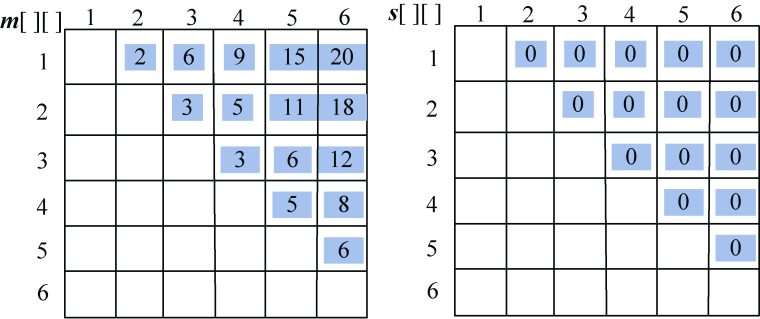
(3)计算4个站点i,i+1,i+2,j(j=i+3)的最优值,并将其存入m[i][j],同时将最优策略记入s[i][j],i=1,2,3。
- i = 1,j=4:
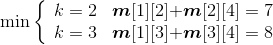
- i =2,j=5:
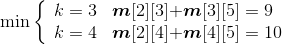
- i =3,j=6:
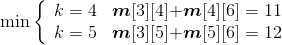
如图4-37所示。
(4)计算5个站点i,i+1,i+2,i+3,j(j=i+4)的最优值,并将其存入m[i][j],同时将最优策略记入s[i][j],i=1、2。
- i = 1,j=5:
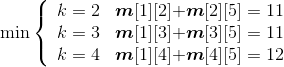
- i = 2,j=6:
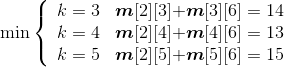
如图4-38所示。
(5)计算6个站点i,i+1,i+2,i+3,i+4,j(j=i+4)的最优值,并将其存入m[i][j],同时将最优策略记入s[i][j],i=1。
- i = 1,j=6:
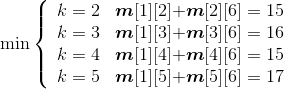
如图4-39所示。
(6)构造最优解
根据存储表格s[][]中的数据来构造最优解,即停靠的站点。
首先输出出发站点1;读取s[1][6]=2,表示在2号站点停靠,即分解为两个子问题:(1,2)和(2,3,4,5,6)。
先看第一个子问题(1,2):读取s[1][2]=0,表示没有停靠任何站点,直接到达2,输出2。
再看第二个子问题(2,3,4,5,6):读取s[2][6]=4,表示在4号站点停靠,即分解为两个子问题:(2,3,4)和(4,5,6)。
先看子问题(2,3,4):读取s[2][4]=0,表示没有停靠任何站点,直接到达4,输出4。
再看子问题(4,5,6):读取s[4][6]=0,表示没有停靠任何站点,直接到达6,输出6。
最终答案是:1——2——4——6。
4.5.4 伪代码详解
(1)最少租金求解函数
设计中n表示有n个出租站,设置二维数组m[][],初始化时用来记录从i到j之间的租金r[][],在不同规模的子问题(d=3,4,…,n)中,按照递推公式计算,如果比原值m[][]小,则更新m[][],同时用s[][]记录停靠的站点号,直接最后得到的r[1][n]即为最后的结果。
1 | void rent() |
(2)最优解构造函数
根据s[][]数组构造最优解,s[i][j]将问题分解为两个子问题(i,…,s[i][j])、(s[i][j],…,j),递归求解这两个子问题。当s[i][j]=0时,说明中间没有经过任何站点,直达站点j,输入j,返回即可。
1 | void print(int i,int j) |
4.5.5 实战演练
1 | //program 4-3 |
算法实现和测试
(1)运行环境
Code::Blocks
Visual C++ 6.0
(2)输入
1 | 请输入站点的个数n:6 |
(3)输出
1 | 花费的最少租金为:15 |
4.5.6 算法解析及优化拓展
1.算法复杂度分析
(1)时间复杂度:由程序可以得出:语句temp=m[i][k]+m[k][j],它是算法的基本语句,在3层for循环中嵌套,最坏情况下该语句的执行次数为O(n3),print()函数算法的时间主要取决于递归,最坏情况下时间复杂度为O(n)。故该程序的时间复杂度为O(n3)。
(2)空间复杂度:该程序的输入数据的数组为r[][],辅助变量为i、j、r、t、k、m[][]、s[][],空间复杂度取决于辅助空间,该程序的空间复杂度为O(n2)。
2.算法优化拓展
如果只是想得到最优值(最少的租金),则不需要s[][]数组;m[][]数组也可以省略,直接在r[][]数组上更新即可,这样空间复杂度减少为O(1)。
4.6 快速计算——矩阵连乘
给定n个矩阵{A1,A 2,A3,…,A n},其中,A i 和A i+1(i=1,2,…,n−1)是可乘的。矩阵乘法如图4-40所示。用加括号的方法表示矩阵连乘的次序,不同的计算次序计算量(乘法次数)是不同的,找出一种加括号的方法,使得矩阵连乘的计算量最小。
例如:
A1是M5×10的矩阵;
A2是M10×100的矩阵;
A3是M100×2的矩阵。
那么有两种加括号的方法:
(1)(A1 A2)A3;
(2)A1(A2 A3)。
第1种加括号方法运算量:5×10×100+5×100×2=6000。
第2种加括号方法运算量:10×100×2+5×10×2=2100。
可以看出,不同的加括号办法,矩阵乘法的运算次数可能有巨大的差别!
4.6.1 问题分析
矩阵连乘问题就是对于给定n个连乘的矩阵,找出一种加括号的方法,使得矩阵连乘的计算量(乘法次数)最小。
看到这个问题,我们需要了解以下内容。
(1)什么是矩阵可乘?
如果两个矩阵, 第1个矩阵的列等于第2个矩阵的行时,那么这两个矩阵是可乘的。 如图4-41所示。
(2)矩阵相乘后的结果是什么?
从图4-41可以看出,两个矩阵相乘的结果矩阵,其行、列分别等于第1个矩阵的行、第2个矩阵的列。如果有很多矩阵相乘呢?如图4-42所示。
多个矩阵相乘的结果矩阵,其行、列分别等于第1个矩阵的行、最后1个矩阵的列。 而且无论矩阵的计算次序如何都不影响它们的结果矩阵。
(3)两个矩阵相乘需要多少次乘法?
例如两个矩阵A3×2、B2×4相乘,结果为C3×4要怎么计算呢?
A矩阵第1行第1个数 * B矩阵第1列第1个数:1×2;
A矩阵第1行第2个数 * B矩阵第1列第2个数:2×3;
两者相加存放在C矩阵第1行第1列:1 × 2+2 × 3。
A矩阵第1行第1个数 * B矩阵第2列第1个数:1×4;
A矩阵第1行第2个数 * B矩阵第2列第2个数:2×6;
两者相加存放在C矩阵第1行第2列:1 × 4+2 × 6。
A矩阵第1行第1个数 * B矩阵第3列第1个数:1×5;
A矩阵第1行第2个数 * B矩阵第3列第2个数:2×9;
两者相加存放在C矩阵第1行第3列:1 × 5+2 × 9。
A矩阵第1行第1个数 * B矩阵第4列第1个数:1×8;
A矩阵第1行第2个数 * B矩阵第4列第2个数:2×10;
两者相加存放在C矩阵第1行第4列:1 × 8+2 × 10。
其他行以此类推。
计算结果如图4-43所示。
可以看出,结果矩阵中每个数都执行了两次乘法运算,有3×4=12个数,一共需要执行2×3×4=24次,两个矩阵A3×2、A2×4相乘执行乘法运算的次数为3×2×4。因此,A m×n、A n×k相乘执行乘法运算的次数为mnk 。
如果穷举所有的加括号方法,那么加括号的所有方案是一个卡特兰数序列,其算法时间复杂度为2n,是指数阶。因此穷举的办法是很糟的,那么能不能用动态规划呢?
下面分析矩阵连乘问题A i A i+1…A j是否具有最优子结构性质。
(1)分析最优解的结构特征
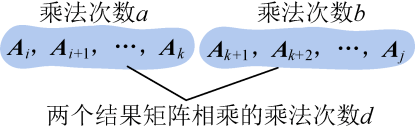
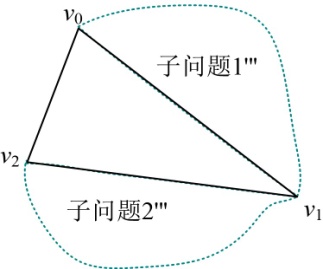
- 假设我们已经知道了在第k个位置加括号会得到最优解,那么原问题就变成了两个子问题:(A i A i+1…A k),(A k+1A k+2…A j),如图4-44所示。
原问题的最优解是否包含子问题的最优解呢?
- 假设A i A i+1…A j的乘法次数是c,(A i A i+1…A k)的乘法次数是a,(A k+1A k+2…A j)的乘法次数是b,(A i A i+1…A k)和(A k+1A k+2…A j)的结果矩阵相乘的乘法次数是d,那么c=a+b+d,无论两个子问题(A i A i+1…A k)、(A k+1A k+2…A j)的计算次序如何,都不影响它们结果矩阵,两个结果矩阵相乘的乘法次数d不变。因此我们只需要证明如果c是最优的,则a和b一定是最优的(即原问题的最优解包含子问题的最优解)。
反证法: 如果a不是最优的,(A i A i+1…A k)存在一个最优解a’,a’<a,那么,a’+b+d<c,所以c不是最优的,这与假设c是最优的矛盾,因此如果c是最优的,则a一定是最优的。同理可证b也是最优的。因此如果c是最优的,则a和b一定是最优的。
因此,矩阵连乘问题具有最优子结构性质。
(2)建立最优值递归式
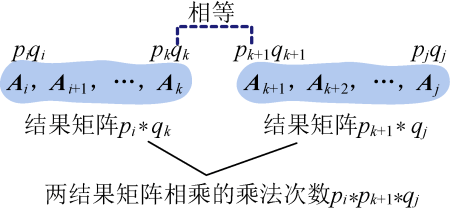
- 用m[i][j]表示A i A i+1…A j矩阵连乘的最优值,那么两个子问题(A i A i+1…A k)、(A k+1A k+2…A j)对应的最优值分别是m[i][k]、m[k+1][j]。剩下的只需要考查(A i A i+1…A k)和(A k+1A k+2…A j)的结果矩阵相乘的乘法次数了。
- 设矩阵A m的行数为pm,列数为qm,m=i,i+1, …,j,且矩阵是可乘的,即相邻矩阵前一个矩阵的列等于下一个矩阵的行(qm= pm+1)。(A i A i+1…A k)的结果是一个pi×qk矩阵,(A k+1A k+2…A j)的结果是一个pk+1*qj矩阵,qk= pk+1,两个结果矩阵相乘的乘法次数是pi*pk+1*qj。如图4-45所示。
- 矩阵连乘最优值递归式:
当i=j时,只有一个矩阵,m[i][j]=0;
当i>j时,
如果用一维数组p[]来记录矩阵的行和列,第i个矩阵的行数存储在数组的第i−1位置,列数存储在数组的第i位置,那么pi*pk+1*qj对应的数组元素相乘为p[i−1]p[k] p[j],原递归式变为:
(3)自底向上计算并记录最优值
先求两个矩阵相乘的最优值,再求3个矩阵相乘的最优值,直到n个矩阵连乘的最优值。
(4)构造最优解
上面得到的最优值只是矩阵连乘的最小的乘法次数,并不知道加括号的次序,需要从记录表中还原加括号次序,构造出最优解,例如A1(A2A3)。
这个问题是一个动态规划求矩阵连乘最小计算量的问题,将问题分为小规模的问题,自底向上,将规模放大,直到得到所求规模的问题的解。
4.6.2 算法设计
采用自底向上的方法求最优值,对于每一个小规模的子问题都求最优值,并记录最优策略(加括号位置),具体算法设计如下。
(1)确定合适的数据结构
采用一维数组p[]来记录矩阵的行和列,第i个矩阵的行数存储在数组的第i−1位置,列数存储在数组的第i位置。二维数组m[][]来存放各个子问题的最优值,二维数组s[][]来存放各个子问题的最优决策(加括号的位置)。
(2)初始化
采用一维数组p[]来记录矩阵的行和列,m[i][i]=0,s[i][i]=0,其中i= 1,2,3,…,n。
(3)循环阶段
- 按照递归关系式计算2个矩阵A i、A i+1相乘时的最优值,j=i+1,并将其存入m[i][j],同时将最优策略记入s[i][j],i=1,2,3,…,n−1。
- 按照递归关系式计算3个矩阵相乘A i、A i+1、A i+2相乘时的最优值,j=i+2,并将其存入m[i][j],同时将最优策略记入s[i][j],i=1,2,3,…,n−2。
- 以此类推,直到求出n个矩阵相乘的最优值m[1][n]。
(4)构造最优解
根据最优决策信息数组s[][]递归构造最优解。s[1][n] 表示A1A2…A n最优解的加括号位置,即(A1A2…As[1][n])(As[1][n]+1…A n),我们在递归构造两个子问题(A1A2…As[1][n])、(As[1][n]+1…A n)的最优解加括号位置,一直递归到子问题只包含一个矩阵为止。
4.6.3 完美图解
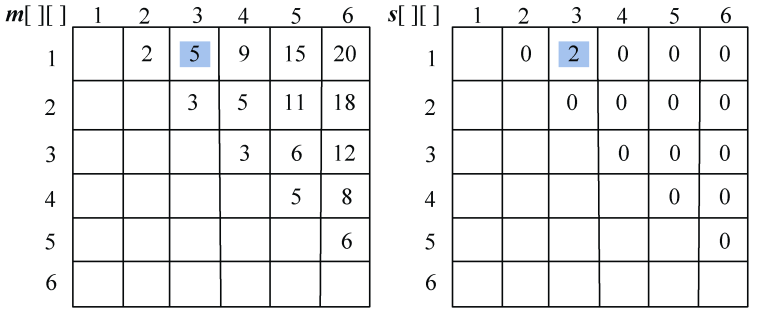
现在我们假设有5个矩阵,如表4-1所示。
| 矩阵 | A1 | A2 | A3 | A4 | A5 |
| :----- | :----- | :----- | :----- | :----- | :----- | :----- | :----- |
| 规模 | 3×5 | 5×10 | 10×8 | 8×2 | 2×4 |
(1)初始化
采用一维数组p[]记录矩阵的行和列,实际上只需要记录每个矩阵的行,再加上最后一个矩阵的列即可,如图4-46所示。m[i][i]=0,s[i][i]=0,其中i= 1,2,3,4,5。
最优值数组m[i][i]=0,最优决策数组s[i][i]=0,其中i= 1,2,3,4,5。如图4-47所示。
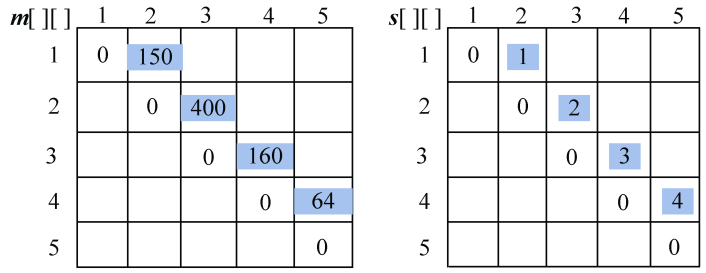
(2)计算两个矩阵相乘的最优值
规模r=2。根据递归式:
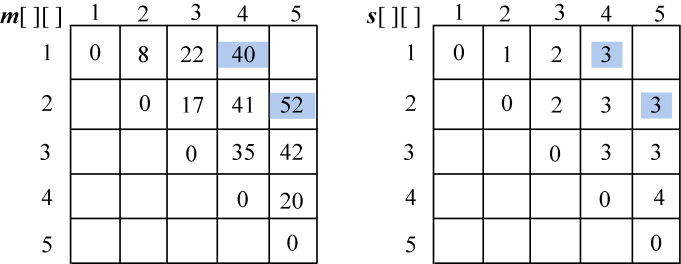
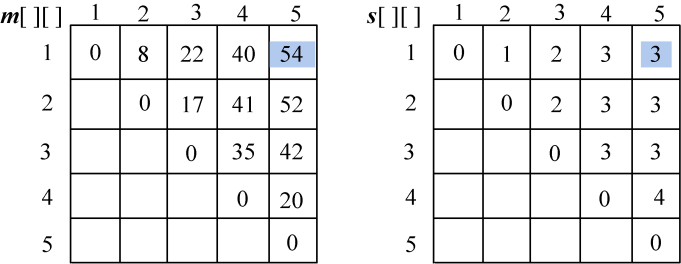
- A1*A2:k=1,m[1][2]=min{ m[1][1]+ m[2][2]+p0p1p2}=150;s[1][2]=1。
- A2*A3:k=2,m[2][3]=min{ m[2][2]+ m[3][3]+p1p2p3}=400;s[2][3]=2。
- A3*A4:k=3,m[3][4]=min{ m[3][3]+ m[4][4]+p2p3p4}=160;s[3][4]=3。
- A4*A5:k=4,m[4][5]=min{ m[4][4]+ m[5][5]+p3p4p5}=64; s[4][5]=4。
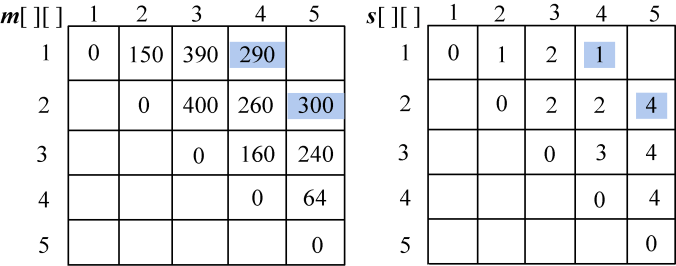
计算完毕,如图4-48所示。
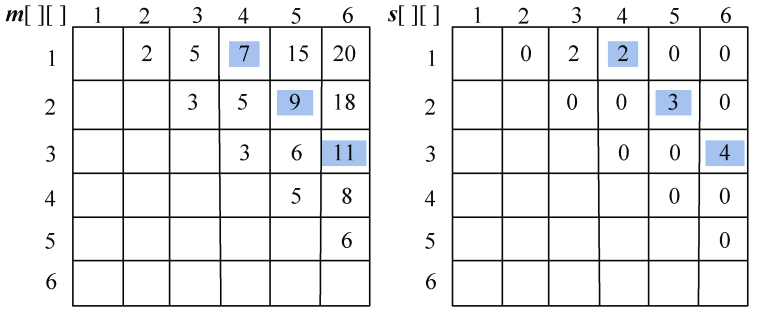
(3)计算3个矩阵相乘的最优值
规模r=3。根据递归式:
- A1*A2*A3:
;
s[1][3]=2。
- A2*A3*A4:
;
s[2][4]=2。
- A3*A4*A5:
;
s[3][5]=4。
计算完毕,如图4-49所示。
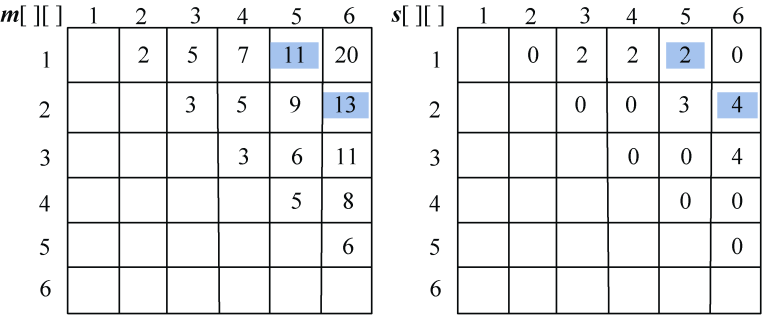
(4)计算4个矩阵相乘的最优值
规模r=4。根据递归式:
- A1*A2*A3*A4:
;
s[1][4]=1。
- A2*A3*A4*A5:
;
s[2][5]=4。
计算完毕,如图4-50所示。
(5)计算5个矩阵相乘的最优值
规模r=5。根据递归式:
- A1*A2*A3*A4*A5:
;
s[1][5]=4。
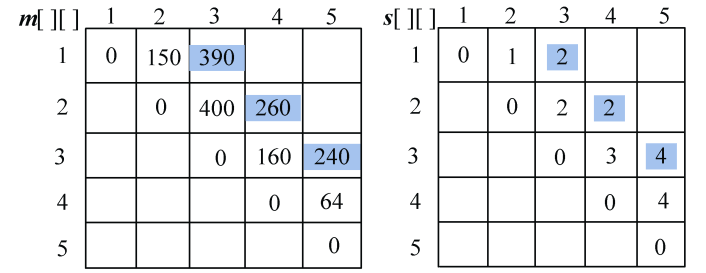
计算完毕,如图4-51所示。
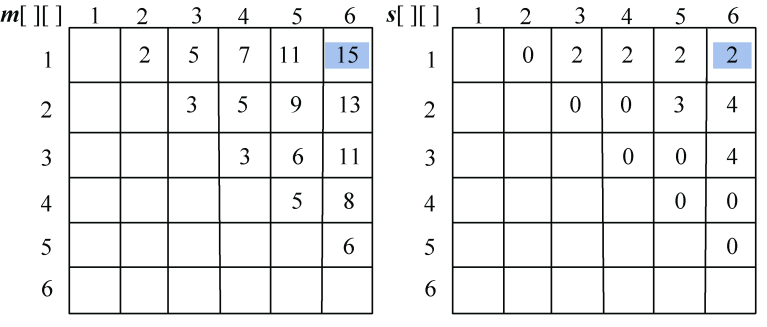
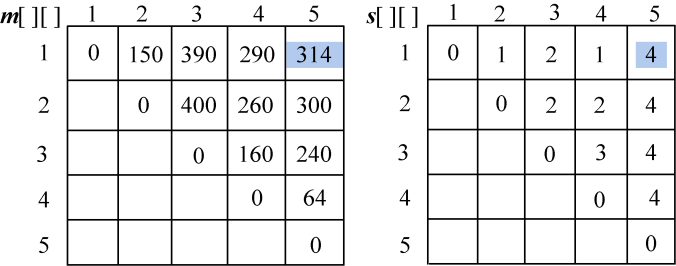
(6)构造最优解
根据最优决策数组s[][]中的数据来构造最优解,即加括号的位置。
首先读取s[1][5]=4,表示在k=4的位置把矩阵分为两个子问题:(A1A2A3A4)、A5。
再看第一个子问题(A1A2A3A4),读取s[1][4]=1,表示在k=1的位置把矩阵分为两个子问题:A1、(A2A3A4)。
子问题A1不用再分解,输出;子问题(A2A3A4),读取s[2][4]=2,表示在k=2的位置把矩阵分为两个子问题:A2、(A3A4)。
子问题A2不用再分解,输出;子问题(A3A4),读取s[3][4]=3,表示在k=3的位置把矩阵分为两个子问题:A3、A4。这两个子问题都不用再分解,输出。
子问题A5不用再分解,输出。
最优解构造过程如图4-52所示。
最优解为:((A1(A2(A3A4)))A5)。
最优值为:314。
4.6.4 伪代码详解
按照算法思想和设计,以下程序将矩阵的行和列存储在一维数组p[],m[][]数组用于存储分成的各个子问题的最优值,s[][]数组用于存储各个子问题的决策点,然后在一个for循环里,将问题分为规模为r的子问题,求每个规模子问题的最优解,那么得到的m[1][n]就是最小的计算量。
(1)矩阵连乘求解函数
首先将数组m[][],s[][]初始化为0,然后自底向上处理不同规模的子问题,r为问题的规模,r= 2;r <= n;r++,当r= 2时,表示矩阵连乘的规模为2,即两个矩阵连乘。求解两个矩阵连乘的最优值和最优策略,根据递归式:
对每一个k值,求解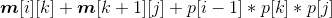
1 | void matrixchain() |
(2)最优解输出函数
根据存储表格s[][]中的数据来构造最优解,即加括号的位置。首先打印一个左括号,然后递归求解子问题print(i, s[i][j]),print(s[i][j]+1,j),再打印右括号,当i=j即只剩下一个矩阵时输出该矩阵即可。
1 | void print(int i,int j) |
4.6.5 实战演练
1 | //program 4-4 |
算法实现和测试
(1)运行环境
Code::Blocks
Visual C++ 6.0
(2)输入
1 | 请输入矩阵的个数 n:5 |
(3)输出
1 | ((A[1](A[2](A[3]A[4])))A[5]) |
4.6.6 算法解析及优化拓展
1.算法复杂度分析
(1)时间复杂度:由程序可以得出:语句 t= m[i][k] + m[k+1][j] +p[i−1]*p[k]*p[j],它是算法的基本语句,在3层for循环中嵌套。最坏情况下,该语句的执行次数为O(n3),print()函数算法的时间主要取决于递归,时间复杂度为O(n)。故该程序的时间复杂度为O(n3)。
(2)空间复杂度:该程序的输入数据的数组为p[],辅助变量为i、j、r、t、k、m[][]、s[][],空间复杂度取决于辅助空间,因此空间复杂度为O(n2)。
2.算法优化拓展
想一想,还有什么办法对算法进行改进,或者有什么更好的算法实现?
4.7 切呀切披萨——最优三角剖分
有一块多边形的披萨饼,上面有很多蔬菜和肉片,我们希望沿着两个不相邻的顶点切成小三角形,并且尽可能少地切碎披萨上面的蔬菜和肉片。
4.7.1 问题分析
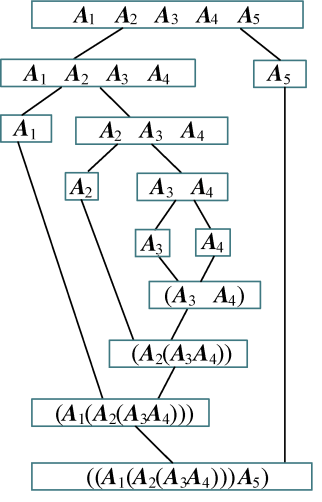
我们可以把披萨饼看作一个凸多边形,凸多边形是指多边形的任意两点的连线均落在多边形的内部或边界上。
(1)什么是凸多边形?
图4-54所示是一个凸多边形,图4-55所示不是凸多边形,因为v1v3的连线落在了多边形的外部。
凸多边形不相邻的两个顶点的连线称为凸多边形的弦。
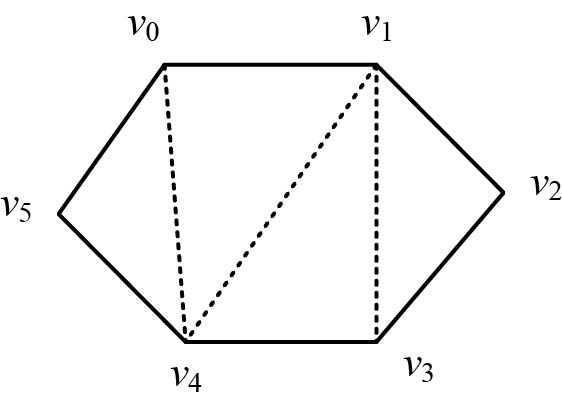
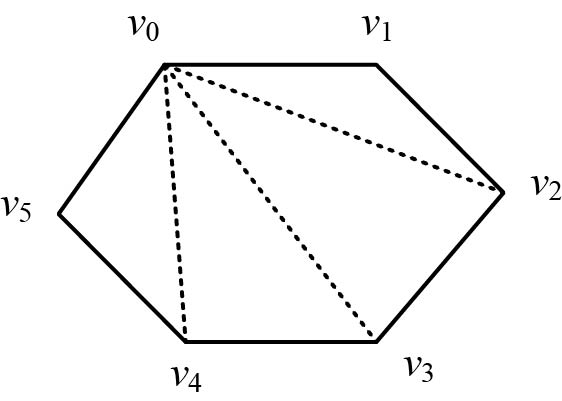
(2)什么是凸多边形三角剖分?
凸多边形的三角剖分是指将一个凸多边形 分割成互不相交的三角形的弦的集合 。图4-56所示的一个三角剖分是{ v0v4,v1v3,v1v4},另一个三角剖分是{ v0v2,v0v3,v0v4},一个凸多边形的三角剖分有很多种。
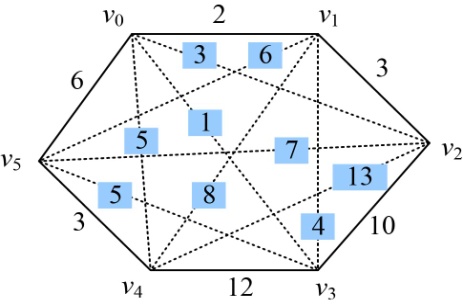
如果我们给定凸多边形及定义在边、弦上的权值,即任意两点之间定义一个数值作为权值。如图4-57所示。
三角形上权值之和是指三角形的3条边上权值之和:
如图4-58所示,。
(3)什么是凸多边形最优三角剖分?
一个凸多边形的三角剖分有很多种,最优三角剖分就是划分的各三角形上权函数之和最小的三角剖分。
再回到切披萨的问题上来,我们可以把披萨看作一个凸多边形,任何两个顶点的连线对应的权值代表上面的蔬菜和肉片数,我们希望沿着两个不相邻的顶点切成小三角形,尽可能少地切碎披萨上面的蔬菜和肉片。那么,该问题可以归结为凸多边形的最优三角剖分问题。
假设把披萨看作一个凸多边形,标注各顶点为{v0,v1,…,vn}。那么怎么得到它的最优三角剖分呢?
首先分析该问题是否具有最优子结构性质。
(1)分析最优解的结构特征
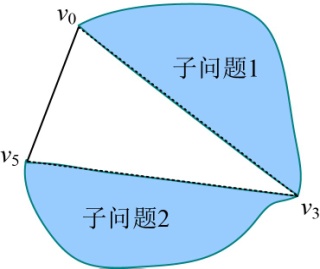
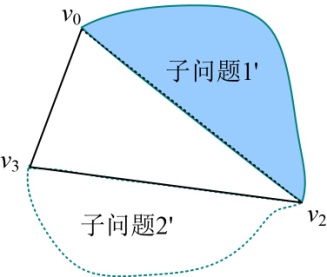
- 假设已经知道了在第k个顶点切开会得到最优解,那么原问题就变成了两个子问题和一个三角形,子问题分别是{v0,v1,…,vk}和{vk,vk+1,…,vn},三角形为v0vkvn,如图4-59所示。
那么原问题的最优解是否包含子问题的最优解呢?
- 假设{v0,v1,…,vn}三角剖分的权值之和是c,{v0,v1,…,vk}三角剖分的权值之和是a,{vk,vk+1,…,vn}三角剖分的权函数之和是b,三角形v0vkvn的权值之和是w(v0vkvn),那么c=a+b+ w(v0vkvn)。因此我们只需要证明如果c是最优的,则a和b一定是最优的(即原问题的最优解包含子问题的最优解)。
反证法: 如果a不是最优的,{v0,v1,…,vk}三角剖分一定存在一个最优解a’,a’<a,那么a’+b+w(v0vkvn)<c,所以c不是最优的,这与假设c是最优的矛盾,因此如果c是最优的,则a一定是最优的。同理可证b也是最优的。因此如果c是最优的,则a和b一定是最优的。
因此,凸多边形的最优三角剖分问题具有最优子结构性质。
(2)建立最优值的递归式
- 用m[i][j]表示凸多边形{vi−1,vi,…,vj}三角剖分的最优值,那么两个子问题{vi−1,vi,…,vk}、{vk,vk+1,…,vj}对应的最优值分别是m[i][k]、m[k+1][j],如图4-60所示,剩下的就是三角形vi−1vkvj的权值之和是w(vi−1vkvj)。
当i=j时,{vi−1,vi,…,vj}就变成了{vi−1,vi },是一条线段,不能形成一个三角形剖分,我们可以将其看作退化的多边形,其权值设置为0。
- 凸多边形三角剖分最优解递归式:
当i=j时,只是一个线段,m[i][j]=0。
当i>j时,,
。
(3)自底向上计算并记录最优值
先求只有3个顶点凸多边形三角剖分的最优值,再求4个顶点凸多边形三角剖分的最优值,直到n个顶点凸多边形三角剖分的最优值。
(4)构造最优解
上面得到的最优值只是凸多边形三角剖分的三角形权值之和最小值,并不知道是怎样剖分的。我们需要从记录表中还原剖分次序,找到最优剖分的弦,由这些弦构造出最优解。
如图4-61所示,如果vk 能够得到凸多边形{vi−1,vi,…,vj}的最优三角剖分,那么我们就找到两条弦vi−1vk和vkvj,把这两条弦放在最优解集合里面,继续求解两个子问题最优三角剖分的弦。
凸多边形最优三角剖分的问题,首先判断该问题是否具有最优子结构性质,有了这个性质就可以使用动态规划,然后分析问题找最优解的递归式,根据递归式自底向上求解,最后根据最优决策表格,构造出最优解。
4.7.2 算法设计
凸多边形最优三角剖分满足动态规划的最优子结构性质,可以从自底向上逐渐推出整体的最优。
(1)确定合适的数据结构
采用二维数组g[][]记录各个顶点之间的连接权值,二维数组m[][]存放各个子问题的最优值,二维数组s[][]存放各个子问题的最优决策。
(2)初始化
输入顶点数n,然后依次输入各个顶点之间的连接权值存储在二维数组g[][]中,令n=n−1(顶点标号从v0开始),m[i][i]=0,s[i][i]=0,其中i= 1,2,3,…,n。
(3)循环阶段
- 按照递归关系式计算3个顶点{vi−1,vi,vi+1}的最优三角剖分,j=i+1,将最优值存入m[i][j],同时将最优策略记入s[i][ j],i= 1,2,3,…,n−1。
- 按照递归关系式计算4个顶点{vi−1,vi,vi+1,vi+2}的最优三角剖分,j=i+2,将最优值存入m[i][ j],同时将最优策略记入s[i][ j],i= 1,2,3,…,n−2。
- 以此类推,直到求出所有顶点 {v0,v1,…,vn} 的最优三角剖分,并将最优值存入m[1][n],将最优策略记入s[1][n]。
(4)构造最优解
根据最优决策信息数组s[][]递归构造最优解,即输出凸多边形最优剖分的所有弦。s[1][n] 表示凸多边形{v0,v1,…,vn} 的最优三角剖分位置,如图4-62所示。
- 如果子问题1为空,即没有一个顶点,说明v0vs[1][n]是一条边,不是弦,不需输出,否则,输出该弦v0vs[1][n]。
- 如果子问题2为空,即没有一个顶点,说明vs[1][n] vn是一条边,不是弦,不需输出,否则,输出该弦vs[1][n] vn。
- 递归构造两个子问题{v0,v1,…,vs[1][n]}和{vs[1][n],v1,…,vn },一直递归到子问题为空停止。
4.7.3 完美图解
以图4-63的凸多边形为例。
(1)初始化
顶点数n=6,令n=n−1=5(顶点标号从v0开始),然后依次输入各个顶点之间的连接权值存储在邻接矩阵 g [i][j]中,其中i,j=0,1,2,3,4,5,如图4-64所示。m[i][i]=0,s[i][i]=0,其中i=1,2,3,4,5,如图4-65所示。
(2)计算3个顶点{vi−1,vi,vi+1}的最优三角剖分,将最优值存入m[i][j],同时将最优策略记入s[i][j],i=1,2,3,4。
根据递归式:
- i=1,j=2:{v0,v1,v2}
- k=1:m[1][2]=min{m[1][1]+m[2][2]+w(v0v1v2)}=8;s[1][2]=1。
- i=2,j=3:{v1,v2,v3}
- k=2:m[2][3]=min{m[2][2]+m[3][3]+w (v1v2v3)}=17;s[2][3]=2。
- i=3,j=4:{v2,v3,v4}
- k=3:m[3][4]=min{m[3][3]+m[4][4]+w (v2v3v4)}=35;s[3][4]=3。
- i=4,j=5:{v3,v4,v5}
- k=4:m[4][5]=min{m[4][4]+m[5][5]+w (v3v4v5)}=20;s[4][5]=4。
计算完毕,如图4-66所示。
(3)计算4个顶点{vi−1,vi,vi+1,vi+2}的最优三角剖分,将最优值存入m[i][j],同时将最优策略记入s[i][j],i=1,2,3。
根据递归式:
- i=1,j=3:{v0,v1,v2,v3}
;
s[1][3]=2。
- i=2,j=4:{v1,v2,v3,v4}
;
s[2][4]=3。
- i=3,j=5:{v2,v3,v4,v5}
;
s[3][5]=3。
计算完毕,如图4-67所示:
(4)计算5个顶点{vi-1,vi,vi+1,vi+2,vi+3}的最优三角剖分,将最优值存入m[i][j],同时将最优策略记入s[i][j],i=1,2。
根据递归式:
- i=1,j=4:{v0,v1,v2,v3,v4}
;
s[1][4]=3。
- i=2,j=5:{v1,v2,v3,v4,v5}
;
s[2][5]=3。
计算完毕,如图4-68所示。
(5)计算6个顶点{vi−1,vi,vi+1,vi+2,vi+3,vi+4}的最优三角剖分,j=i+4,将最优值存入m[i][j],同时将最优策略记入s[i][j],i=1。
根据递归式:
- i=1,j=5:{v0,v1,v2,v3,v4,v5}
;
s[1][5]=3。
计算完毕,如图4-69所示。
(6)构造最优解
根据最优决策信息数组s[][]递归构造最优解,即输出凸多边形最优剖分的所有弦。s[1][5] 表示凸多边形{v0,v1,…,v5} 的最优三角剖分位置,从图4-69最优决策数组可以看出,s[1][5]=3,如图4-70所示。
- 因为v0~v3中有结点,所以子问题1不为空,输出该弦v0v3。
- 因为v3~v5中有结点,所以子问题2不为空,输出该弦v3v5。
- 递归构造子问题1:{v0,v1,v2,v3},读取s[1][3]=2,如图4-71所示。
因为v0~v2中有结点,所以子问题1’不为空,输出该弦v0v2。
递归构造子问题1’:{v0,v1,v2 },读取s[1][2]=1,如图4-72所示。
因为v0~v1中没有结点,子问题1’''为空,v0v1是一条边,不是弦,不输出。
因为v1~v2中没有结点,子问题2’''为空,v1v2是一条边,不是弦,不输出。
递归构造子问题2’:{ v2,v3 }。
因为v2~v3中没有结点,子问题2’为空,v2v3是一条边,不是弦,不输出。
- 递归构造子问题2:{v3,v4,v5},读取s[4][5]=4,如图4-73所示。
因为v3~v4中没有结点,子问题1’'为空,v3v4是一条边,不是弦,不输出。
因为v4~v5中没有结点,子问题2’'为空,v4v5是一条边,不是弦,不输出。
因此,该凸多边形三角剖分最优解为:v0v3,v3v5,v0v2。
4.7.4 伪代码详解
(1)凸多边形三角剖分求解函数
首先将数组m[][]、s[][]初始化为0,然后自底向上处理不同规模的子问题,d为i到j的规模,d=2;d<=n;d++,当d=2时,实际上是3个点,因为m[i][j]表示的是{vi−1,vi,vj}。求解3个顶点凸多边形三角剖分的最优值和最优策略,根据递归式:
对每一个k值,求解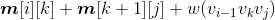
1 | void Convexpolygontriangulation() |
(2)最优解输出函数
我们首先从s[][]数组中读取s[i][j],然后判断子问题1是否为空。若s[i][j]>i,表示i到s[i][j]之间存在顶点,子问题1不为空,那么vi−1vs[i][j]是一条弦,输出{vi−1vs[i][j]};判断子问题2是否为空,若j>s[i][j]+1,表示s[i][j]+1到j之间存在顶点,子问题2不为空,那么vs[i][j]+1 vj是一条弦,输出{vs[i][j]+1vj}。递归求解子问题1和子问题2,直到i=j时停止。
1 | void print(int i , int j) // 输出所有的弦 |
4.7.5 实战演练
1 | //program 4-5 |
算法实现和测试
(1)运行环境
Code::Blocks
Visual C++ 6.0
(2)输入
1 | 6 |
(3)输出
1 | 54 |
4.7.6 算法解析及优化拓展
1.算法复杂度分析
(1)时间复杂度:由程序可以得出语句 t= m[i][k] + m[k+1][j] + g[i−1][i] + g[i][j] + g[i−1] [j],它是算法的基本语句,在3层for循环中嵌套,最坏情况下该语句的执行次数为O(n3),print()函数算法的时间主要取决于递归,最坏情况下时间复杂度为O(n)。故该程序的时间复杂度为O(n3)。
(2)空间复杂度:该程序的输入数据的数组为g[][],辅助变量为i、j、r、t、k、m[][]、s[][],空间复杂度取决于辅助空间,因此空间复杂度为O(n2)。
2.算法优化拓展
这个问题尽管和矩阵连乘问题表达的含义不同,但递归式是完全相同的,那么程序代码就可以参考矩阵连乘的代码了。
想一想,还有什么办法对算法进行改进,或者有什么更好的算法实现?
4.8 小石子游戏——石子合并
一群小孩子在玩小石子游戏,游戏有两种玩法。
(1)路边玩法
有n堆石子堆放在路边,现要将石子有序地合并成一堆,规定每次只能移动相邻的两堆石子合并,合并花费为新合成的一堆石子的数量。求将这N堆石子合并成一堆的总花费(最小或最大)。
(2)操场玩法
一个圆形操场周围摆放着n堆石子,现要将石子有序地合并成一堆,规定每次只能移动相邻的两堆石子合并,合并花费为新合成的一堆石子的数量。求将这N堆石子合并成一堆的总花费(最小或最大)。
4.8.1 问题分析
本题初看可以使用贪心法来解决,但是因为有必须相邻两堆才能合并这个条件在,用贪心法就无法保证每次都能取到所有堆中石子数最少(最多)的两堆。
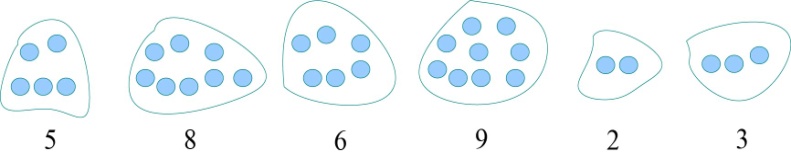
下面以操场玩法为例:假设有n=6堆石子,每堆的石子个数分别为3、4、6、5、4、2。
如果使用贪心法求最小花费,应该是如下的合并步骤:
第1次合并 3 4 6 5 4 2 2,3合并花费是5
第2次合并 5 4 6 5 4 5,4合并花费是9
第3次合并 9 6 5 4 5,4合并花费是9
第4次合并 9 6 9 9,6合并花费是15
第5次合并 15 9 15,9合并花费是24
总得分=5+9+9+15+24=62
但是如果采用如下合并方法,却可以得到比上面花费更少的方法:
第1次合并 3 4 6 5 4 2 3,4合并花费是7
第2次合并 7 6 5 4 2 7,6合并花费是13
第3次合并 13 5 4 2 4,2合并花费是6
第4次合并 13 5 6 5,6合并花费是11
第5次合并 13 11 13,11合并花费是24
总花费=7+13+6+11+24=61
显然利用贪心法来求解错误的,贪心算法在子过程中得出的解只是局部最优,而不能保证全局的值最优,因此本题不可以使用贪心法求解。
如果使用暴力穷举的办法,会有大量的子问题重复,这种做法是不可取的,那么是否可以使用动态规划呢?我们要分析该问题是否具有最优子结构性质,它是使用动态规划的必要条件。
1.路边玩法
如果n−1次合并的全局最优解包含了每一次合并的子问题的最优解,那么经这样的n−1次合并后的花费总和必然是最优的,因此我们就可以通过动态规划算法来求出最优解。
首先分析该问题是否具有最优子结构性质。
(1)分析最优解的结构特征
- 假设已经知道了在第k堆石子分开可以得到最优解,那么原问题就变成了两个子问题,子问题分别是{ai,a2,…,ak}和{ ak+1,…,aj},如图4-75所示。
那么原问题的最优解是否包含子问题的最优解呢?
- 假设已经知道了n堆石子合并起来的花费是c,子问题1{ ai,a2,…,ak }石子合并起来的花费是a,子问题2{ ak+1,…,aj}石子合并起来的花费是b,{ ai,a2,…,aj }石子数量之和是w(i,j),那么c=a+b+ w(i,j)。因此我们只需要证明如果c是最优的,则a和b一定是最优的(即原问题的最优解包含子问题的最优解)。
反证法: 如果a不是最优的,子问题1{ ai,a2,…,ak }一定存在一个最优解a’,a’<a,那么a’+b+ w(i,j)<c,这与我们的假设c是最优的矛盾,因此如果c是最优的,则a一定是最优的。同理可证b也是最优的。因此如果c是最优的,则a和b一定是最优的。
因此,路边玩法小石子合并游戏问题具有最优子结构性质。
(2)建立最优值递归式
设Min[i][j]代表从第i堆石子到第j堆石子合并的最小花费,Min[i][k]代表从第i堆石子到第k堆石子合并的最小花费,Min[k+1][j]代表从第k+1堆石子到第j堆石子合并的最小花费,w(i,j)代表从i堆到j堆的石子数量之和。列出递归式:
Max[i][j] 代表从第 i 堆石子到第 j 堆石子合并的最大花费,Max[i][k] 代表从第 i 堆石子到第 k堆石子合并的最大花费,Max[k+1][j] 代表从第 k+1堆石子到第 j 堆石子合并的最大花费,w(i,j)代表从i堆到j堆的石子数量之和。列出递归式:
2.操场玩法
如果把路边玩法看作直线型石子合并问题,那么操场玩法就属于圆型石子合并问题。圆型石子合并经常转化为直线型来求。也就是说,把圆形结构看成是长度为原规模两倍的直线结构来处理。如果操场玩法原问题规模为n,所以相当于有一排石子a1,a2,…,an,a1,a2,…,an−1,该问题规模为2n−1,如图4-76所示。然后就可以用线性的石子合并问题的方法求解,求最大值的方法和求最小值的方法是一样的。最后,从 规模是 n 的最优值 找出 最小值或最大值 即可。
4.8.2 算法设计
1.路边玩法
假设有n堆石子,一字排开,合并相邻两堆的石子,每合并两堆石子有一个花费,最终合并后的最小花费和最大花费。
(1)确定合适的数据结构
采用一维数组a[i]来记录第i堆石子(ai)的数量;sum[i]来记录前i堆(a1,a2,…,ai)石子的总数量;二维数组Min[i][j]、Max[i][j]来记录第i堆到第j堆ai,ai+1,…,ai堆石子合并的最小花费和最大花费。
(2)初始化
输入石子的堆数n,然后依次输入各堆石子的数量存储在a[i]中,令Min[i][i]=0,Max[i][i]=0,sum[0]=0,计算sum[i],其中i= 1,2,3,…,n。
(3)循环阶段
- 按照递归式计算2堆石子合并{ai,ai+1}的最小花费和最大花费,i=1,2,3,…,n−1。
- 按照递归式计算3堆石子合并{ai,ai+1,ai+2}的最小花费和最大花费,i=1,2,3,…,n−2。
- 以此类推,直到求出所有堆{a1,…,an}的最小花费和最大花费。
(4)构造最优解
Min[1][n]和Max[1][n]是n堆石子合并的最小花费和最大花费。如果还想知道具体的合并顺序,需要在求解的过程中记录最优决策,然后逆向构造最优解,可以使用类似矩阵连乘的构造方法,用括号来表达合并的先后顺序。
2.操场玩法
圆型石子合并经常转化为直线型来求,也就是说,把圆形结构看成是长度为原规模两倍的直线结构来处理。如果操场玩法原问题规模为n,所以相当于有一排石子a1,a2,…,an,a1,a2,…,an−1,该问题规模为2n−1,然后就可以用线性的石子合并问题的方法求解,求最小花费和最大花费的方法是一样的。最后,从规模是n的最优值找出最小值即可。即要从规模为n的最优值Min[1][n],Min[2][n+1],Min[3][n+2],…,Min[n][2n−1]中找最小值作为圆型石子合并的最小花费。
从 规模是 n 的最优值 Max[1][n],Max[2][n+1],Max[3][n+2],…,Max[n][2n−1] 中找 最大值 作为圆型石子合并的最大花费。
4.8.3 完美图解
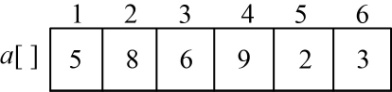
如图4-77所示,以6堆石子的路边玩法为例。
(1)初始化
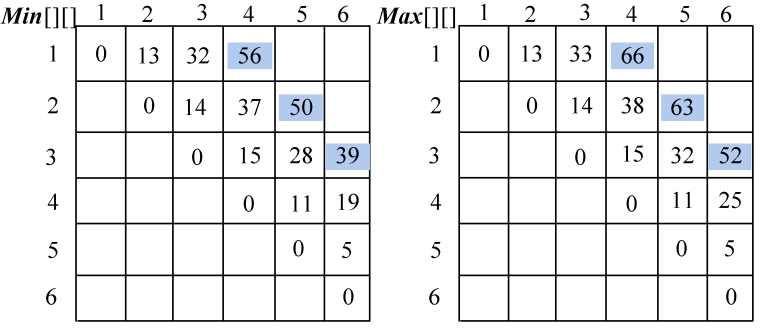
输入石子的堆数n,然后依次输入各堆石子的数量存储在a[i]中,如图4-78所示。
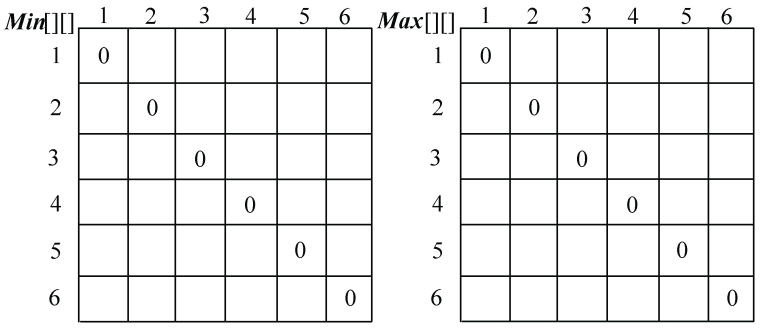
Min[i][j]和Max[i][j]来记录第i堆到第j堆ai,ai+1,…,ai堆石子合并的最小花费和最大花费。令Min[i][i]=0,Max[i][i]=0,如图4-79所示。
sum[i]为前i堆石子数量总和,sum[0]=0,计算sum[i],其中i= 1,2,3,…,n,如图4-80所示。
原递归公式中的w(i,j)代表从i堆到j堆的石子数量之和,可以用直接查表法sum[j] −sum[i−1]求解,如图4-81所示。这样就不用每次遇到w(i,j)都计算一遍了,这也是动态规划思想的显现!
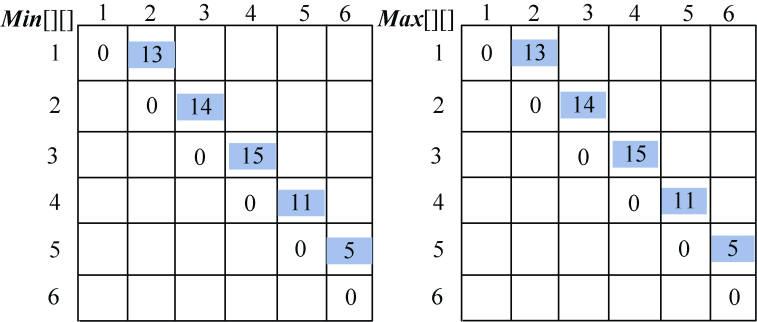
(2)按照递归式计算两堆石子合并{ai,ai+1}的最小花费和最大花费,i=1,2,3,4,5。如图4-82所示。
- i=1,j=2:{a1,a2}
k=1:Min[1][2]=Min[1][1]+Min[2][2]+sum[2] −sum[0]=13;
** Max**[1][2]=Max[1][1]+Max[2][2]+sum[2] −sum[0]=13。
- i=2,j=3:{a2,a3}
k=2:Min[2][3]=Min[2][2]+Min[3][3]+sum[3] −sum[1]=14;
** Max**[2][3]=Max[2][2]+Max[3][3]+sum[3] −sum[1]=14。
- i=3,j=4:{a3,a4}
k=3:Min[3][4]=Min[3][3]+Min[4][4]+sum[4] −sum[2]=15;
** Max**[3][4]=Max[3][3]+Max[4][4]+sum[4] −sum[2]=15。
- i=4,j=5:{a4,a5}
k=4:Min[4][5]=Min[4][4]+Min[5][5]+sum[5] −sum[3]=11;
** Max**[4][5]=Max[4][4]+Max[5][5]+sum[5] −sum[3]=11。
- i=5,j=6:{a5,a6}
k=5:Min[5][6]=Min[5][5]+Min[6][6]+sum[6] −sum[4]=5;
** Max**[5][6]=Max[5][5]+Max[6][6]+sum[6] −sum[4]=5。
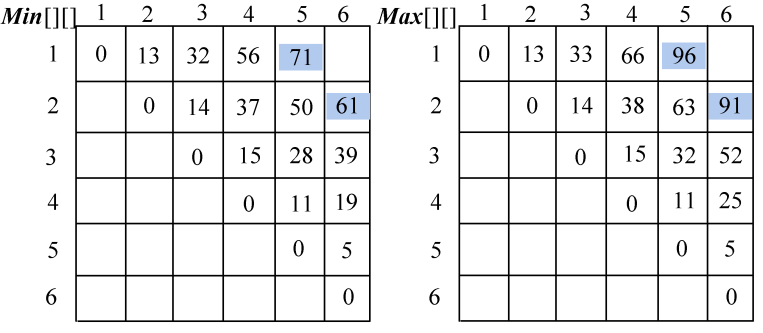
(3)按照递归式计算3堆石子合并{ai,ai+1,ai+2}的最小花费和最大花费,i=1,2,3,4,如图4-83所示。
- i=1,j=3:{ a1,a2,a3}
Min[1][3]= 32;Max[1][3]=33。
- i=2,j=4:{ a2,a3,a4}
Min[2][4]= 37;Max[2][4]=38。
- i=3,j=5:{ a3,a4,a5}
Min[3][5]= 28;Max[3][5]=32。
- i=4,j=6:{ a4,a5,a6}
Min[4][6]= 19;Max[4][6]=25。
(4)按照递归式计算4堆石子合并{ai,ai+1,ai+2,ai+3}的最小花费和最大花费,i=1,2,3,如图4-84所示。
- i=1,j=4:{ a1,a2,a3,a4}
Min[1][4]= 56;Max[1][4]=66。
- i=2,j=5:{ a2,a3,a4,a5}
Min[2][5]=50;Max[2][5]=63。
- i=3,j=6:{ a3,a4,a5,a6}
Min[3][6]=39;Max[3][6]=52。
(5)按照递归式计算5堆石子合并{ai,ai+1,ai+2,ai+3,ai+4}的最小花费和最大花费,i=1,2,如图4-85所示。
- i=1,j=5:{ a1,a2,a3,a4,a5}
Min[1][5]=71;Max[1][5]=96。
- i=2,j=6:{ a2,a3,a4,a5,a6}
Min[2][6]=61;Max[3][6]=9。
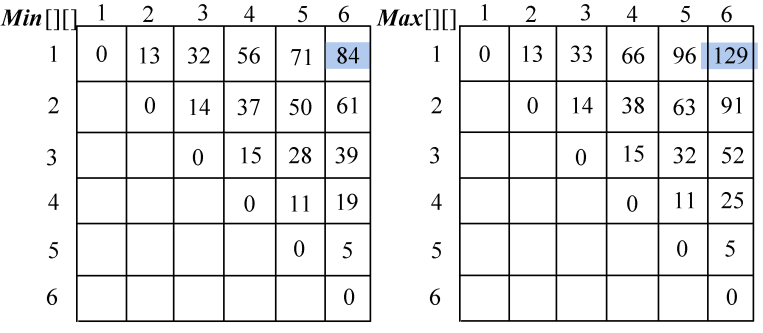
(6)按照递归式计算6堆石子合并{a1,a2,a3,a4,a5,a6}的最小花费和最大花费,如图4-86所示。
- i=1,j=6:{ a1,a2,a3,a4,a5,a6}
Min[1][6]=84;Max[1][6]=129。
4.8.4 伪代码详解
(1)路边玩法
首先初始化Min[i][i]=0,Max[i][i]=0,sum[0]=0,计算sum[i],其中i= 1,2,3,…,n。
循环阶段:
按照递归式计算2堆石子合并{ai,ai+1}的最小花费和最大花费,i=1,2,3,…,n−1。
按照递归式计算3堆石子合并{ai,ai+1,ai+2}的最小花费和最大花费,i=1,2,3,…,n−2。
以此类推,直到求出所有堆{a1,…,an}的最小花费和最大花费。
1 | void straight(int a[],int n) |
(2)操场玩法
圆型石子合并经常转化为直线型来求,也就是说,把圆形结构看成是长度为原规模两倍的直线结构来处理。如果操场玩法原问题规模为n,所以相当于有一排石子a1,a2,…,an,a1,a2,…,an−1,该问题规模为2n−1,然后就可以用线性的石子合并问题的方法求解,求最小花费和最大花费的方法是一样的。最后,从最优解中找出规模是n的最优解即可。
即要从规模为n的最优解Min[1][n],Min[2][n+1],Min[3][n+2],…,Min[n][2n−1]中找最小值作为圆型石子合并的最小花费。
从Max[1][n],Max[2][n+1],Max[3][n+2],…,Max[n][2n−1] 中找出最大值作为圆型石子合并的最大花费。
1 | void Circular(int a[],int n) |
4.8.5 实战演练
1 | //program 4-6 |
算法实现和测试
(1)运行环境
Code::Blocks
(2)输入
1 | 请输入石子的堆数 n: |
(3)输出
1 | 路边玩法(直线型)最小花费为:84 |
4.8.6 算法解析及优化拓展
1.算法复杂度分析
(1)时间复杂度:由程序可以得出语句Min[i][j] = min(Min[i][j], Min[i][k] + Min[k+1][j] + tmp),它是算法的基本语句,在3层for循环中嵌套,最坏情况下该语句的执行次数为O(n3),故该程序的时间复杂度为O(n3)。
(2)空间复杂度:该程序的辅助变量为Min[][]、Max[][],空间复杂度取决于辅助空间,故空间复杂度为O(n2)。
2.算法优化拓展
对于石子合并问题,如果按照普通的区间动态规划进行求解,时间复杂度是O(n3),但最小值可以用四边形不等式(见附录F)优化。
s[i][j]表示取得最优解Min[i][j]的最优策略位置。
k的取值范围缩小了很多,原来是区间[i,j),现在变为区间[s[i][j−1],s[i+1][j])。如图4-87所示。
经过优化,算法时间复杂度可以减少至O(n2)。
注意:最大值有一个性质,即总是在两个端点的最大者中取到。
即Max[i][j] = max(Max[i][j−1], Max[i+1][j]) + sum[i][j]
经过优化,算法时间复杂度也可以减少至O(n2)。
优化后算法:
1 | //program 4-6-1 |
(1)时间复杂度:在get_Min()函数中,虽然有3层for循环语句,但并不是有3层for语句的执行次数就是O(n3),我们分析其执行次数为:
因为公式中的j=i+v−1,所以:
故get_Min()的时间复杂度为O(n2)。
在get_Max()函数中,有两层for循环语句嵌套,时间复杂度也是O(n2)。
(2)空间复杂度:空间复杂度取决于辅助空间,空间复杂度为O(n2)。
4.9 大卖场购物车1——0-1背包问题
央视有一个大型娱乐节目——购物街,舞台上模拟超市大卖场,有很多货物,每个嘉宾分配一个购物车,可以尽情地装满购物车,购物车中装的货物价值最高者取胜。假设有n个物品和1个购物车,每个物品i对应价值为vi,重量wi,购物车的容量为W(你也可以将重量设定为体积)。每个物品只有1件,要么装入,要么不装入,不可拆分。在购物车不超重的情况下,如何选取物品装入购物车,使所装入的物品的总价值最大?最大价值是多少?装入了哪些物品?
4.9.1 问题分析
有n个物品和购物车的容量,每个物品的重量为w[i],价值为v[i],购物车的容量为W。选若干个物品放入购物车,使价值最大,可表示如下。
约束条件:
目标函数:
问题归结为求解满足约束条件,使目标函数达到最大值的解向量X={x1,x2,…,xn}。
该问题就是经典的0-1背包问题,我们在第2章贪心算法中已经知道背包问题(可切割)可以用贪心算法求解,而0-1背包问题使用贪心算法有可能得不到最优解(参看2.4.6节)。因为物品的不可切割性,无法保证能够装满背包,所以采用每次装价值/重量比最高的贪心策略是不可行的。
那么是否能够使用动态规划呢?
首先分析该问题是否具有最优子结构性质。
(1)分析最优解的结构特征
- 假设已经知道了X={x1,x2,…,xn}是原问题{a1,a2,…,an}的最优解,那么原问题去掉第一个物品就变成了子问题{a2,a3,…,an},如图4-89所示。
子问题的约束条件和目标函数如下。
约束条件:
目标函数:
- 我们只需要证明:X’={x2,…,xn}是子问题{a2,…,an}的最优解,即证明了最优子结构性质。
反证法: 假设X’={ x2,…,xn}不是子问题{ a2,…,an}的最优解,{ y2,…,yn}是子问题的最优解,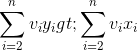
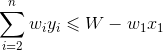

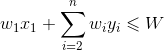
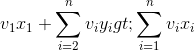
该问题是否具有最优子结构性质。
(2)建立最优值的递归式
可以对每个物品依次检查是否放入或者不放入,对于第i个物品的处理状态:
用c[i][j]表示前i件物品放入一个容量为j的购物车可以获得的最大价值。
- 不放入第i件物品,xi=0,装入购物车的价值不增加。那么问题就转化为“前i−1件物品放入容量为j的背包中”,最大价值为c[i−1][j]。
- 放入第i件物品,xi=1,装入购物车的价值增加vi。
那么问题就转化为“前i−1件物品放入容量为j−w[i]的购物车中”,此时能获得的最大价值就是c[i−1][j−w[i]],再加上放入第i件物品获得的价值v[i]。即c[i−1][j−w[i]]+ v[i]。
购物车容量不足,肯定不能放入;购物车容量足,我们要看放入、不放入哪种情况获得的价值更大。
4.9.2 算法设计
有n个物品,每个物品的重量为w[i],价值为v[i],购物车的容量为W。选若干个物品放入购物车,在不超过容量的前提下使获得的价值最大。
(1)确定合适的数据结构
采用一维数组w[i]、v[i]来记录第i个物品的重量和价值;二维数组用c[i][j]表示前i件物品放入一个容量为j的购物车可以获得的最大价值。
(2)初始化
初始化c[][]数组0行0列为0:c[0][j]=0,c[i][0] =0,其中i=0,1,2,…,n,j=0,1,2,…,W。
(3)循环阶段
- 按照递归式计算第1个物品的处理情况,得到c[1][j],j=1,2,…,W。
- 按照递归式计算第2个物品的处理情况,得到c[2][j],j=1,2,…,W。
- 以此类推,按照递归式计算第n个物品的处理情况,得到c[n][j],j=1,2,…,W。
(4)构造最优解
c[n][W]就是不超过购物车容量能放入物品的最大价值。如果还想知道具体放入了哪些物品,就需要根据c[][]数组逆向构造最优解。我们可以用一维数组x[i]来存储解向量。
- 首先i=n,j=W,如果c[i][j]>c[i−1][j],则说明第n个物品放入了购物车,令x[n]=1,j−=w[n];如果c[i][j]≤c[i−1][j],则说明第n个物品没有放入购物车,令x[n]=0。
- i−−,继续查找答案。
- 直到i=1处理完毕。
这时已经得到了解向量(x[1],x[2],…,x[n]),可以直接输出该解向量,也可以仅把x[i]=1的货物序号i输出。
4.9.3 完美图解
假设现在有5个物品,每个物品的重量为(2,5,4,2,3),价值为(6,3,5,4,6),如图4-90所示。购物车的容量为10,求在不超过购物车容量的前提下,把哪些物品放入购物车,才能获得最大价值。
(1)初始化
c[i][j]表示前i件物品放入一个容量为j的购物车可以获得的最大价值。初始化c[][]数组0行0列为0:c[0][j]=0,c[i][0] =0,其中i=0,1,2,…,n,j=0,1,2,…,W。如图4-91所示。
按照递归式计算第1个物品(i=1)的处理情况,得到c[1][j],j=1,2,…,W。
w[1]=2,v[1]=6,如图4-92所示。
- j=1时,c[1][1]=c[0][1]=0;
- j=2时,c[1][2]=max{c[0][2],c[0][0]+6}=6;
- j=3时,c[1][3]=max{c[0][3],c[0][1]+6}=6;
- j=4时,c[1][4]=max{c[0][4],c[0][2]+6}=6;
- j=5时,c[1][5]=max{c[0][5],c[0][3]+6}=6;
- j=6时,c[1][6]=max{c[0][6],c[0][4]+6}=6;
- j=7时,c[1][7]=max{c[0][7],c[0][5]+6}=6;
- j=8时,c[1][8]=max{c[0][8],c[0][6]+6}=6;
- j=9时,c[1][9]=max{c[0][9],c[0][7]+6}=6;
- j=10时,c[1][10]=max{c[0][10],c[0][8]+6}=6。
(2)按照递归式计算第1个物品(i=2)的处理情况,得到c[2][j],j=1,2,…,W。
w[2]=5,v[2]=3,如图4-93所示。
- j=1时,c[2][1]=c[1][1]=0;
- j=2时,c[2][2]=c[1][2]=6;
- j=3时,c[2][3]=c[1][3]=6;
- j=4时,c[2][4]=c[1][4]=6;
- j=5时,c[2][5]=max{c[1][5],c[1][0]+3}=6;
- j=6时,c[2][6]=max{c[1][6],c[1][1]+3}=6;
- j=7时,c[2][7]=max{c[1][7],c[1][2]+3}=9;
- j=8时,c[2][8]=max{c[1][8],c[1][3]+3}=9;
- j=9时,c[2][9]=max{c[1][9],c[1][4]+3}=9;
- j=10时,c[1][10]=max{c[1][10],c[1][5]+3}=9。
(3)按照递归式计算第1个物品(i=3)的处理情况,得到c[3][j],j=1,2,…,W。
w[3]=4,v[3]=5,如图4-94所示。
- j=1时,c[3][1]=c[2][1]=0;
- j=2时,c[3][2]=c[2][2]=6;
- j=3时,c[3][3]=c[2][3]=6;
- j=4时,c[3][4]=max{c[2][4],c[2][0]+5}=6;
- j=5时,c[3][5]=max{c[2][5],c[2][1]+5}=6;
- j=6时,c[3][6]=max{c[2][6],c[2][2]+5}=11;
- j=7时,c[3][7]=max{c[2][7],c[2][3]+5}=11;
- j=8时,c[3][8]=max{c[2][8],c[2][4]+5}=11;
- j=9时,c[3][9]=max{c[2][9],c[2][5]+5}=11;
- j=10时,c[3][10]=max{c[2][10],c[2][6]+5}=11。
(4)按照递归式计算第1个物品(i=4)的处理情况,得到c[4][j],j=1,2,…,W。
w[4]=2,v[4]=4,如图4-95所示。
- j=1时,c[4][1]=c[3][1]=0;
- j=2时,c[4][2]=max{c[3][2],c[3][0]+4}=6;
- j=3时,c[4][3]=max{c[3][3],c[3][1]+4}=6;
- j=4时,c[4][4]=max{c[3][4],c[3][2]+4}=10;
- j=5时,c[4][5]=max{c[3][5],c[3][3]+4}=10;
- j=6时,c[4][6]=max{c[3][6],c[3][4]+4}=11;
- j=7时,c[4][7]=max{c[3][7],c[3][5]+4}=11;
- j=8时,c[4][8]=max{c[3][8],c[3][6]+4}=15;
- j=9时,c[4][9]=max{c[3][9],c[3][7]+4}=15;
- j=10时,c[4][10]=max{c[3][10],c[3][8]+4}=15。
(5)按照递归式计算第1个物品(i=5)的处理情况,得到c[5][j],j=1,2,…,W。
w[5]=3,v[5]=6,如图4-96所示。
- j=1时,c[5][1]=c[4][1]=0;
- j=2时,c[5][2]=c[4][2]=6;
- j=3时,c[5][3]=max{c[4][3],c[4][0]+6}=6;
- j=4时,c[5][4]=max{c[4][4],c[4][1]+6}=10;
- j=5时,c[5][5]=max{c[4][5],c[4][2]+6}=12;
- j=6时,c[5][6]=max{c[4][6],c[4][3]+6}=12;
- j=7时,c[5][7]=max{c[4][7],c[4][4]+6}=16;
- j=8时,c[5][8]=max{c[4][8],c[4][5]+6}=16;
- j=9时,c[5][9]=max{c[4][9],c[4][6]+6}=17;
- j=10时,c[5][10]=max{c[4][10],c[4][7]+6}=17。
(6)构造最优解
首先读取c[5][10]>c[4][10],说明第5个物品装入了购物车,即x[5]=1,j=10−w[5]=7;
去找c[4][7]=c[3][7],说明第4个物品没装入购物车,即x[4]=0;
去找c[3][7]>c[2][7],说明第3个物品装入了购物车,即x[3]=1,j= j−w[3]=3;
去找c[2][3]=c[1][3],说明第2个物品没装入购物车,即x[2]=0;
去找c[1][3]>c[0][3],说明第1个物品装入了购物车,即x[1]=1,j= j−w[1]=1。
如图4-97所示。
4.9.5 实战演练
1 | //program 4-7 |
算法实现和测试
(1)运行环境
Code::Blocks
Visual C++ 6.0
(2)输入
1 | 请输入物品的个数n:5 |
(3)输出
1 | 装入购物车的最大价值为:17 |
4.9.6 算法解析及优化拓展
1.算法复杂度分析
(1)时间复杂度:算法中有主要的是两层嵌套的for循环,其时间复杂度为O(n*W)。
(2)空间复杂度:由于二维数组c[n][W],所以空间复杂度为O(n*W)。
2.算法优化拓展
如何实现优化改进呢?首先有一个主循环i=1,2,…,N,每次算出来二维数组c[i][0~W]的所有值。那么,如果只用一个数组dp[0~W],能不能保证第i次循环结束后dp[j]中表示的就是我们定义的状态c[i][j]呢?c[i][j]由c[i−1][j]和c[i−1] [j−w[i]]两个子问题递推而来,能否保证在递推c[i][j]时(也即在第i次主循环中递推dp[j]时)能够得到c[i−1][j]和c[i−1][j−w[i]]的值呢?事实上,这要求在每次主循环中以j=W,W−1,…,1,0的顺序倒推dp[j],这样才能保证递推dp[j]时dp[j−c[i]]保存的是状态c[i −1][j−w[i]]的值。
伪代码如下:
1 | for i=1..n |
其中,dp[j]=max{dp[j],dp[j−w[i]]}就相当于转移方程c[i][j]=max{c[i−1][j],c[i−1][j− w[i]]},因为这里的dp[j−w[i]]就相当于原来的c[i−1][j−w[i]]。
1 | //program 4-7-1 |
其实我们可以缩小范围,因为只有当购物车的容量大于等于物品的重量时才要更新(dp[j] = max(dp[j],dp[j−w[i]]+v[i])),如果当购物车的容量小于物品的重量时,则保持原来的值(相当于原来的c[i−1][j])即可。因此第2个for语句可以是for(j=W;j>=w[i];j−−),而不必搜索到j=0。
1 | void opt2(int n,int W) |
我们还可以再缩小范围,确定搜索的下界bound,搜索下界取w[i]与剩余容量的最大值,sum[n] −sum[i−1]表示i~n的物品重量之和。W−(sum[n] −sum[i−1])表示剩余容量。
因为只有购物车容量超过下界时才要更新(dp[j] = max(dp[j],dp[j−w[i]]+v[i])),如果购物车容量小于下界,则保持原来的值(相当于原来的c[i−1][j])即可。因此第2个for语句可以是for(j=W;j>=bound;j−−),而不必搜索到j=0。
1 | void opt3(int n,int W) |
4.10 快速定位——最优二叉搜索树
给定n个关键字组成的有序序列S={s1,s2,…,sn},关键字结点称为实结点。对每个关键字查找的概率是pi,查找不成功的结点称为虚结点,对应{e0,e1,…,en},每个虚结点的查找概率为qi。e0表示小于s1的值,en大于sn的值。所有结点查找概率之和为1。求最小平均比较次数的二叉搜索树(最优二叉搜索树)。
举例说明:给定一个有序序列S={5,9,12,15,20,24},这些数的查找概率分别是p1、p2、p3、p4、p5、p6。在实际中,有可能有查找不成功的情况,例如要在序列中查找x=2,那么我们就会定位在5的前面,查找不成功,相当于落在了虚结点e0的位置。要在序列中查找x=18,那么就会定位在15~20,查找不成功,相当于落在了虚结点e4的位置。
4.10.1 问题分析
无论是查找成功还是查找不成功,都需要若干次比较才能判断出结果,那么如何查找才能使平均比较次数最小呢?
- 如果使用顺序查找,能不能使平均查找次数最小呢?
- 因为序列是有序的,顺序查找有点笨,折半查找怎样呢?
- 折半查找是在查找概率相等的情况下折半的,查找概率不等的情况又如何呢?
- 在有序、查找概率不同的情况下,采用二叉搜索树能否使平均比较次数最小呢?
- 如何构建最优二叉搜索树?
首先我们要了解二叉搜索树。
二叉搜索树(Binary Search Tree,BST),又称为二叉查找树,它是一棵二叉树(每个结点最多有两个孩子),而且左子树结点<根结点,右子树结点>根结点。
最优二叉搜索树(Optimal Binary Search Tree,OBST)是搜索成本最低的二叉搜索树,即平均比较次数最少。
例如,关键字{s1,s2,…,s6}的搜索概率是{p1,p2,…,p6},查找不成功的结点{e0,e1,…,e6}的搜索概率为{q0,q1,…,q6},其对应的数值如表4-2所示。
接下来,我们通过构建不同的二叉搜索树来分别看其搜索成本(平均比较次数)。
第1种二叉搜索树如图4-100所示。
首先分析关键字结点的搜索成本,搜索每一个关键字需要 比较的次数是其所在的深度+1 。例如关键字5,需要比较1次(深度为0),查找成功;关键字12,需要首先和树根5比较,比5大,找其右子树,和右子树的根9比较,比9大,找其右子树,和右子树的根12比较,相等,查找成功,比较了3次(结点12的深度为2)。因此每个关键字结点的搜索成本=(结点的深度+1)*搜索概率=(depth(si)+1)*pi。
我们再看虚结点,即查找不成功的情况的搜索成本,每一个虚结点需要 比较的次数是其所在的深度 。虚结点e0需要比较1次(深度为1),即和数据5比较,如果小于5,则落入虚结点e0位置,查找失败。虚结点e1需要比较2次(深度为2),需要首先和树根5比较,比5大,找其右子树,和右子树的根9比较,比9小,找其左子树,则落入虚结点e1位置,查找失败,比较了2次(虚结点e1的深度为2)。因此每个虚结点的搜索成本=结点的深度*搜索概率=(depth(ei))*qi。
二叉搜索树1的搜索成本为:
图4-100的搜索成本为:
接下来看第2个二叉搜索树,如图4-101所示。
图4-101的搜索成本为:
第1个二叉搜索树相当于顺序查找(高度最大),第2个二叉搜索树相当于折半查找(平衡树),我们再看第3个二叉搜索树,如图4-102所示。
图4-102的搜索成本为:
第3个图搜索成本又降到了2.52,有没有可能继续降低呢?
可能很多人会想到,搜索概率大的离根越近,那么总的成本就会更低,这其实就是哈夫曼思想。但是因为二叉搜索树需要满足(左子树<根,右子树>根)的性质,那么每次选取时就不能保证一定搜索概率大的结点。所以哈夫曼思想无法构建最优二叉搜索树。那么怎么找到最优解呢?我们很难确定目前得到的就是最优解,如果采用暴力穷举所有的情况,一共有O(4n/n3/2)棵不同的二叉搜索树,这可是指数级的数量!显然是不可取的。
那么如何才能构建一棵最优二叉搜索树呢?
我们来分析该问题是否具有最优子结构性质:
(1)分析最优解的结构特征
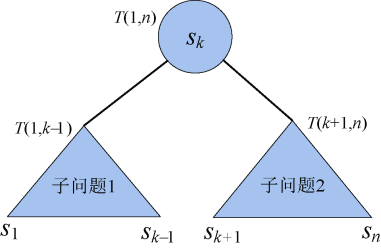
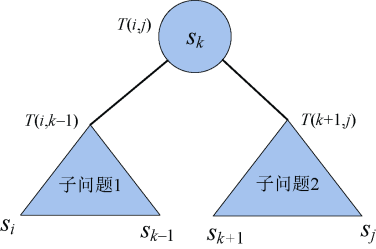
- 原问题为有序序列{s1,s2,…,sn},对应虚结点是{e0,e1,…,en}。假设我们已经知道了sk是二叉搜索树T(1,n)的根,那么原问题就变成了两个子问题:{s1,s2,…,sk-1}和{e0,e1,…,ek−1}构成的左子树T(1,k−1),{sk+1,sk+2,…,sn}和{ek,ek+1,…,en}构成的右子树T(k+1,n)。如图4-103所示。
- 我们只需要证明:如果T(1,n)是最优二叉搜索树,那么它的左子树T(1,k−1)和右子树T(k+1,n)也是最优二叉搜索树。即证明了最优子结构性质。
反证法: 假设T’ (1,k−1)是比T(1,k−1)更优的二叉搜索树,则T’(1,k−1)的搜索成本比T(1,k−1)的搜索成本小,因此由T’ (1,k−1)、sk、T(k+1,n) 组成的二叉搜索树T’ (1,n)的搜索成本比T(1,n)的搜索成本小。T’ (1,n)是最优二叉搜索树,与假设T(1,n)是最优二叉搜索树矛盾。问题得证。
(2)建立最优值的递归式
先看看原问题最优解和子问题最优解的关系:用c[i][j]表示{si,si+1,…,sj}和{ei−1,ei,…,ej}构成的最优二叉搜索树的搜索成本。
- 两个子问题(如图4-104所示)的搜索成本分别是c[i][k−1]和c[k+1][j]。
子问题1包含的结点:{si,si+1,…,sk−1}和{e i−1,ei,…,ek−1}。
子问题2包含的结点:{sk+1,sk+2,…,sj}和{ek,ek+1,…,ej}。
- 把两个子问题和sk一起构建成一棵二叉搜索树,如图4-105所示。
在构建的新树中,左子树和右子树中所有的结点深度增加了1,因为实结点搜索成本=(深度+1)搜索概率p,虚结点搜索成本=深度搜索概率q。
左子树和右子树中所有的结点深度增加了1,相当于搜索成本 增加了 这些结点的搜索概率之和, 加上 sk结点的搜索成本pk,总的增加成本用w[i][j]表示。
所有结点顺序排列一起:{ei−1,si,ei,…,sk,ek,…,sj,ej},它们的概率之和为:
w[i][j]=qi−1+pi+qi+…+ pk+qk+…+pj+qj
最优二叉搜索树的搜索成本为:
c[i][j]= c[i][k−1]+c[k+1][j]+ w[i][j]
因为我们并不确定k的值到底是多少,因此在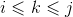
(3)因此最优二叉搜索树的最优值递归式:
w[i][j]也可以使用递推的形式,而没有必要每次都从qi-1加到qj。
这同样也是动态规划的查表法。
4.10.2 算法设计
采用自底向上的方法求最优解,分为不同规模的子问题,对于每一个小的决策都求最优
(1)确定合适的数据结构
采用一维数组p[]、q[]分别记录实结点和虚结点的搜索概率,c[i][j]表示最优二叉搜索树T(i,j)的搜索成本,w[i][j]表示最优二叉搜索树T(i,j)中的所有实结点和虚结点的搜索概率之和,s[i][j]表示最优二叉搜索树T(i,j)的根节点序号。
(2)初始化
输入实结点的个数n,然后依次输入实结点的搜索概率存储在p[i]中,依次输入虚结点的搜索概率存储在q[i]中。令c[i][i−1]=0.0,w[i][i−1]=q[i−1],其中i= 1,2,3,…,n+1。
(3)循环阶段
- 按照递归式计算元素规模是1的{si}(j=i)的最优二叉搜索树搜索成本c[i][j],并记录最优策略,即树根s[i][j],i= 1,2,3,…,n。
- 按照递归式计算元素规模是2的{si,si+1}(j=i+1)的最优二叉搜索树搜索成本c[i][j],并记录最优策略,即树根s[i][j],i= 1,2,3,…,n−1。
- 以此类推,直到求出所有元素{s1,…,sn} 的最优二叉搜索树搜索成本c[1][n]和最优策略s[1][n]。
(4)构造最优解
- 首先读取s[1][n],令k=s[1][n],输出sk为最优二叉搜索树的根。
- 判断如果k−1<1,表示虚结点ek−1是sk的左子树;否则,递归求解左子树Construct_ Optimal_BST(1,k−1,1)。
- 判断如果k≥n,输出虚结点ek是sk的右孩子;否则,输出s[k+1][n]是sk的右孩子,递归求解右子树Construct_Optimal_BST(k+1,n,1)。
4.10.3 完美图解
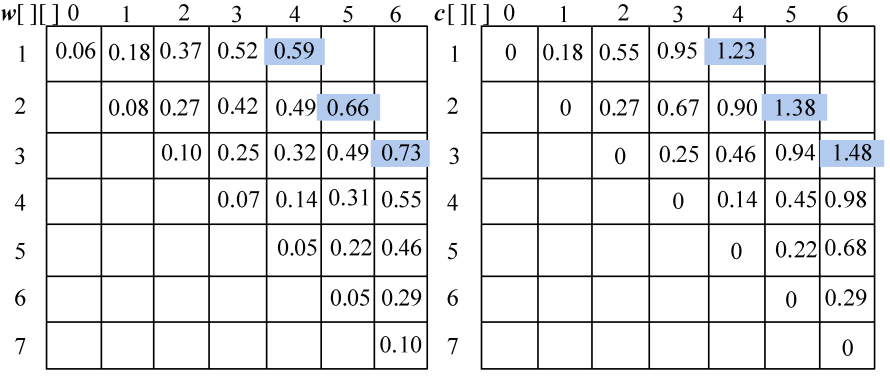
假设我们现在有6个关键字{s1,s2,…,s6}的搜索概率是{p1,p2,…,p6},查找不成功的结点{e0,e1,…,e6}的搜索概率为{q0,q1,…,q6},其对应的数值如图4-106和图4-107所示。
采用一维数组p[]、q[]分别记录实结点和虚结点的搜索概率,c[i][j]表示最优二叉搜索树T(i,j)的搜索成本,w[i][j]表示最优二叉搜索树T(i,j)中的所有实结点和虚结点的搜索概率之和,s[i][j]表示最优二叉搜索树T(i,j)的根节点序号,即取得最小值时的k值。
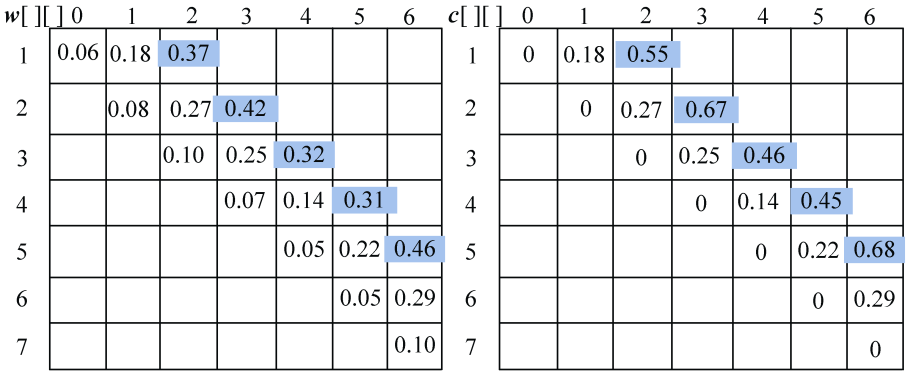
(1)初始化
n=6,令c[i][i−1]=0.0,w[i][i−1]=q[i−1],其中i=1,2,3,…,n+1,如图4-108所示。
(2)按照递归式计算元素规模是1的{si}(j=i)的最优二叉搜索树搜索成本c[i][j],并记录最优策略,即树根s[i][j],i= 1,2,3,…,n。
- i=1,j=1:k=1。
为了形象表达,我们把虚结点和实结点的搜索概率按顺序放在一起,用圆圈和阴影部分表示w[][],如图4-109所示。
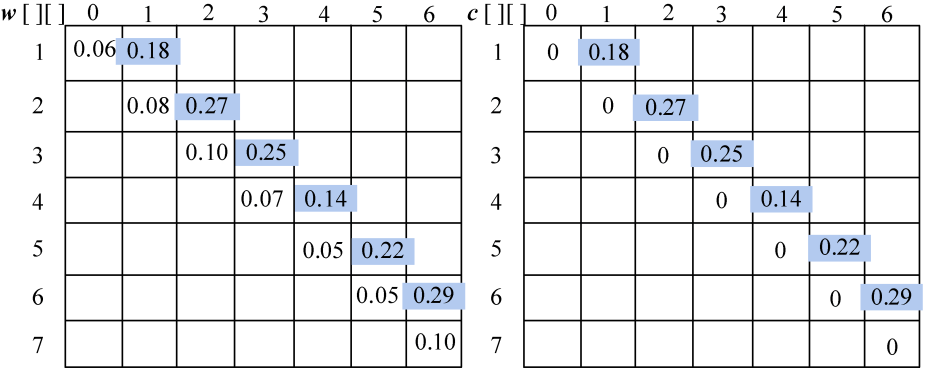
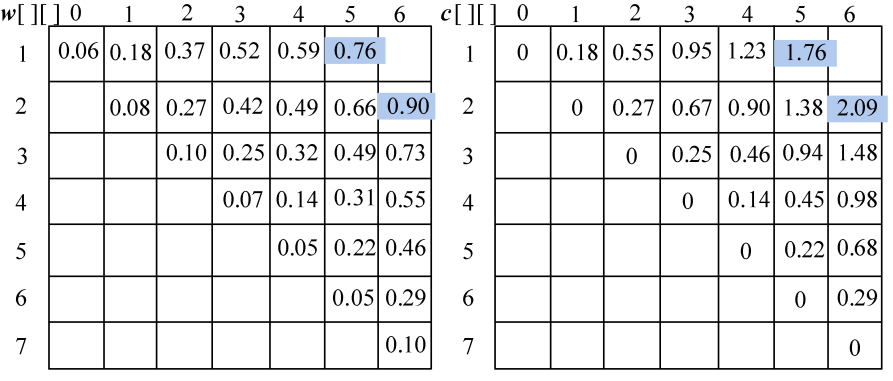
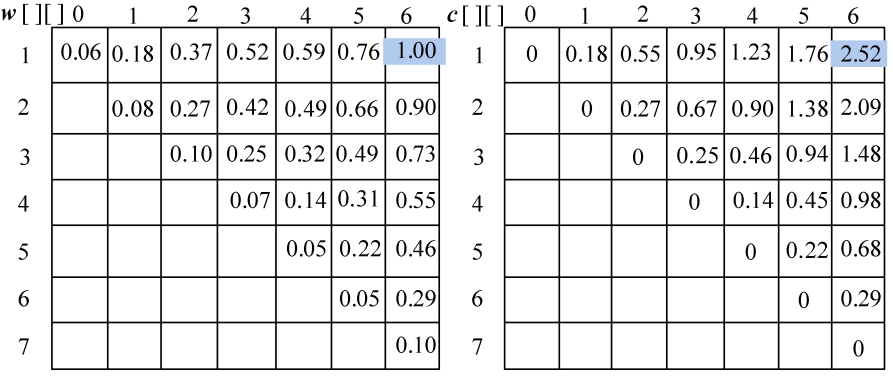
w[1][1]= w[1][0]+p1+q1=0.06+0.04+0.08=0.18;
c[1][1]= min{c[1][0],c[2][1] }+ w[1][1] =0.18;
s[1][1]=1。
- i=2,j=2:k=2。如图4-110所示。
w[2][2]= w[2][1]+p2+q2=0.08+0.09+0.10=0.27;
c[2][2]= min{c[2][1],c[3][2] }+ w[2][2] =0.27;
s[2][2]=2。
- i=3,j=3:k=3。如图4-111所示。
w[3][3]= w[3][2]+p3+q3=0.10+0.08+0.07=0.25;
c[3][3]= min{c[3][2],c[4][3] }+ w[3][3] =0.25;
s[3][3]=3。
- i=4,j=4:k=4。如图4-112所示。
w[4][4]= w[4][3]+p4+q4=0.07+0.02+0.05=0.14;
c[1][1]= min{c[1][0],c[2][1] }+ w[1][1] =0.14;
s[4][4]=4。
- i=5,j=5:k=5。如图4-113所示。
w[5][5]= w[5][4]+p5+q5=0.05+0.12+0.05=0.22;
c[5][5]= min{c[5][4],c[6][5] }+ w[5][5] =0.22;
s[5][5]=5。
- i=6,j=6:k=6。如图4-114所示。
w[6][6]= w[6][5]+p6+q6=0.05+0.14+0.10=0.29;
c[6][6]= min{c[6][5],c[7][6] }+ w[6][6] =0.29;
s[6][6]=6。
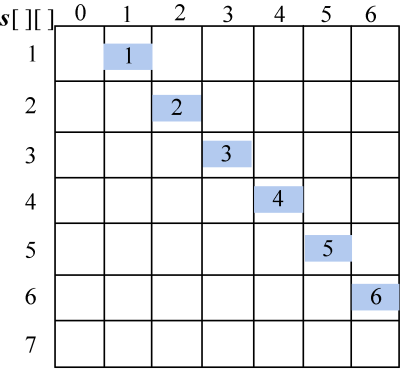
计算完毕,概率之和以及最优二叉树搜索成本如图4-115所示。最优策略如图4-116所示。
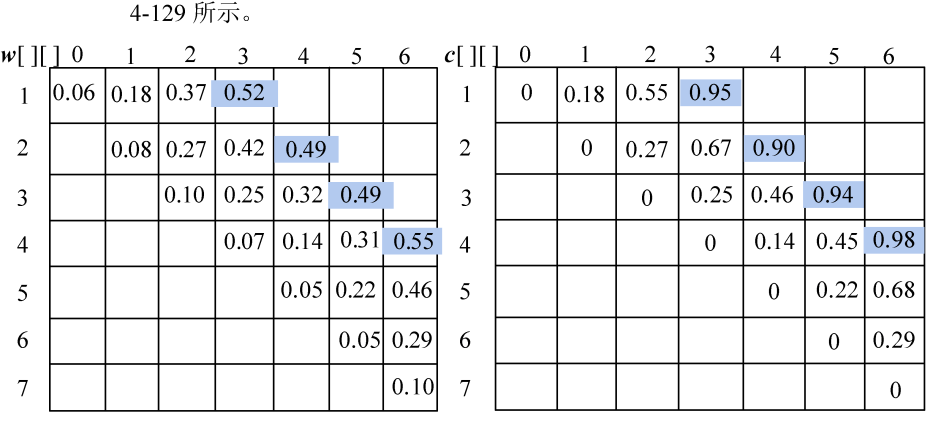
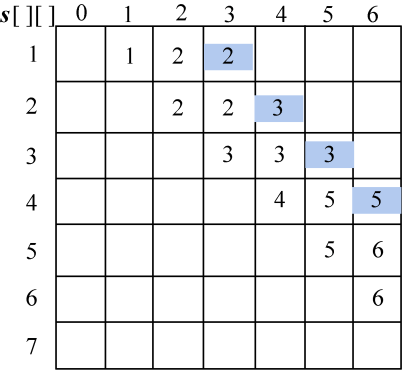
(3)按照递归式计算元素规模是2的{si,si+1}(j=i+1)的最优二叉搜索树搜索成本c[i][j],并记录最优策略,即树根s[i][j],i= 1,2,3,…,n−1。
- i=1,j=2。如图4-117所示。
w[1][2]= w[1][1]+p2+q2=0.18+0.09+0.10=0.37;
;
s[1][2]=2。
- i=2,j=3。如图4-118所示。
w[2][3]= w[2][2]+p3+q3=0.27+0.08+0.07=0.42;
;
s[2][3]=2。
- i=3,j=4。如图4-119所示。
w[3][4]= w[3][3]+p4+q4=0.25+0.02+0.05=0.32;
;
s[3][4]=3。
- i=4,j=5。如图4-120所示。
w[4][5]= w[4][4]+p5+q5=0.14+0.12+0.05=0.31;
;
s[4][5]=5。
- i=5,j=6。如图4-121所示。
w[5][6]= w[5][5]+p6+q6=0.22+0.14+0.10=0.46;
;
s[5][6]=6。
计算完毕。概率之和以及最优二叉树搜索成本如图4-122所示,最优策略如图4-123所示。
(4)按照递归式计算元素规模是3的{si,si+1,si+2}(j=i+2)的最优二叉搜索树搜索成本c[i][j],并记录最优策略,即树根s[i][j],i=1,2,3,4。
- i=1,j=3。如图4-124所示。
w[1][3]= w[1][2]+p3+q3=0.37+0.08+0.07=0.52;
;
s[1][3]=2。
- i=2,j=4。如图4-125所示。
w[2][4]= w[2][3]+p4+q4=0.42+0.02+0.05=0.49;
;
s[2][4]=3。
- i=3,j=5。如图4-126所示。
w[3][5]= w[3][4]+p5+q5=0.32+0.12+0.05=0.49;
;
s[3][5]=3。
- i=4,j=6。如图4-127所示。
w[4][6]= w[4][5]+p6+q6=0.31+0.14+0.10=0.55;
;
s[4][6]=5。
计算完毕。概率之和以及最优二叉树搜索成本如图4-128所示,最优策略如图4-129所示。
(5)按照递归式计算元素规模是4的{si,si+1,si+2,si+3}(j=i+3)的最优二叉搜索树搜索成本c[i][j],并记录最优策略,即树根s[i][j],i=1,2,3。
- i=1,j=4。如图4-130所示。
w[1][4]= w[1][3]+p4+q4=0.52+0.02+0.05=0.59;
;
s[1][4]=2。
- i=2,j=5。如图4-131所示。
w[2][5]= w[2][4]+p5+q5=0.49+0.12+0.05=0.66;
;
s[2][5]=3。
- i=3,j=6。如图4-132所示。
w[3][6]= w[3][5]+p6+q6=0.49+0.14+0.10=0.73;
;
s[3][6]=5。
计算完毕。概率之和以及最优二叉树搜索成本如图4-133所示,最优策略如图4-134所示。
(6)按照递归式计算元素规模是5的{si,si+1,si+2,si+3,si+4}(j=i+4)的最优二叉搜索树搜索成本c[i][j],并记录最优策略,即树根s[i][j],i=1,2。
- i=1,j=5。如图4-135所示。
w[1][5]= w[1][4]+p5+q5=0.59+0.12+0.05=0.76;
;
s[1][5]=3。
- i=2,j=6。如图4-136所示。
w[2][6]= w[2][5]+p6+q6=0.66+0.14+0.10=0.90;
;
s[2][6]=5。
计算完毕。概率之和以及最优二叉树搜索成本如图4-137所示,最优策略如图4-138所示。
(7)按照递归式计算元素规模是6的{si,si+1,si+2,si+3,si+4,si+5}(j=i+5)的最优二叉搜索树搜索成本c[i][j],并记录最优策略,即树根s[i][j],i=1。
- i=1,j=6。如图4-139所示。
w[1][6]= w[1][5]+p6+q6=0.76+0.14+0.10=1.00;
;
s[1][6]=5。
计算完毕。概率之和以及最优二叉树搜索成本如图4-140所示,最优策略如图4-141所示。
(8)构造最优解
- 首先读取s[1][6]=5,k=5,输出s5为最优二叉搜索树的根。
判断如果k−1≥1,读取s[1][4]=2,输出s2为s5的左孩子;递归求解左子树T(1,4);判断如果k<6,读取s[6][6]=6,输出s6为s5的右孩子;递归求解右子树T(6,6),如图4-142所示。
- 递归求解左子树T(1,4)。
首先读取s[1][4]=2,k=2。
判断如果k−1≥1,读取s[1][1]=1,输出s1为s2的左孩子;判断如果k<4,读取s[3][4]=3,输出s3为s2的右孩子;递归求解右子树T(3,4),如图4-143所示。
- 递归求解左子树T(1,1)。
首先读取s[1][1]=1,k=1。
判断如果k−1<1,输出e0为s1的左孩子;判断如果k≥1,输出e1为s1的右孩子,如图4-144所示。
- 递归求解右子树T(3,4)。
首先读取s[3][4]=3,k=3。
判断如果k−1<3,输出e2为s3的左孩子;判断如果k<4,读取s[4][4]=4,输出s4为s3的右孩子;递归求解右子树T(4,4),如图4-145所示。
- 递归求解右子树T(4,4)。
首先读取s[4][4]=4,k=4。
判断如果k−1<4,输出e3为s4的左孩子;判断如果k≥4,输出e4为s4的右孩子,如图4-146所示。
- 递归求解右子树T(6,6)。
首先读取s[6][6]=6,k=6。
判断如果k−1<6,输出e5为s6的左孩子;判断如果k≥6,输出e6为s6的右孩子,如图4-147所示。
4.10.4 伪代码详解
(1)构建最优二叉搜索树
采用一维数组p[]、q[]分别记录实结点和虚结点的搜索概率,c[i][j]表示最优二叉搜索树T(i,j)的搜索成本,w[i][j]表示最优二叉搜索树T(i,j)中的所有实结点和虚结点的搜索概率之和,s[i][j]表示最优二叉搜索树T(i,j)的根节点序号。首先初始化,令c[i][i−1]=0.0,w[i][i−1]=q[i−1],其中i= 1,2,3,…,n+1。按照递归式计算元素规模是1的{si}(j=i)的最优二叉搜索树搜索成本c[i][j],并记录最优策略,即树根s[i][j],i=1,2,3,…,n。按照递归式计算元素规模是2的{si,si+1}(j=i+1)的最优二叉搜索树搜索成本c[i][j],并记录最优策略,即树根s[i][j],i=1,2,3,…,n−1。以此类推,直到求出所有元素{s1,…,sn} 的最优二叉搜索树搜索成本c[1][n]和最优策略s[1][n]。
1 | void Optimal_BST() |
(2)构造最优解
Construct_Optimal_BST(int i,int j,bool flag)表示构建从结点i到结点j的最优二叉搜索树。首次调用时,flag=0、i=1、j=n,表示首次构建,读取的第一个数值s[1][n]为树根,其他递归调用flag=1。
Construct_Optimal_BST(int i,int j,bool flag):首先读取s[i][j],令k=s[i][j],判断如果k−1<i,表示虚结点ek−1是sk的左子树;否则,递归求解左子树Construct_Optimal_BST(i,k−1,1)。判断如果k≥j,输出虚结点ek是sk的右孩子;否则,输出s[k+1][j]是sk的右孩子,递归求解右子树Construct_Optimal_BST(k +1,j,1)。
1 | void Construct_Optimal_BST(int i,int j,bool flag) |
4.10.5 实战演练
1 | //program 4-8 |
算法实现和测试
(1)运行环境
Code::Blocks
Visual C++ 6.0
(2)输入
1 | 请输入关键字的个数n:6 |
(3)输出
1 | 最小的搜索成本为:2.52 |
4.10.6 算法解析及优化拓展
1.算法复杂度分析
(1)时间复杂度:算法中有3层嵌套的for循环,其时间复杂度为O(n3)。
(2)空间复杂度:使用了3个二维数组求解c[i][j]、w[i][j]、s[i][j],所以空间复杂度为O(n2)。
2.算法优化拓展
如果按照普通的区间动态规划进行求解,时间复杂度是O(n3),但可以用四边形不等式优化。
!/524.gif)
s[i][j]表示取得最优解c[i][j]的最优策略位置。
k的取值范围缩小了很多,原来是区间[i,j],现在变为区间[s[i][j−1],s[i+1][j]]。经过优化,算法时间复杂度可以减少至O(n2),时间复杂度的计算可参看4.8.6节。
优化后算法:
1 | //program 4-8-1 |
4.11 动态规划算法秘籍
本章通过8个实例讲解了动态规划的解题过程。动态规划求解最优化问题时需要考虑两个性质:最优子结构和子问题重叠。只要满足最优子结构性质就可以使用动态规划,如果还具有子问题重叠,则更能彰显动态规划的优势。判断可以使用动态规划后,就可以分析其最优子结构特征,找到原问题和子问题的关系,从而得到最优解递归式。然后按照最优解递归式自底向上求解,采用备忘机制(查表法)有效解决子问题重叠,重复的子问题不需要重复求解,只需查表即可。
动态规划的关键总结如下。
(1)最优子结构判定
- 作出一个选择。
- 假定已经知道了哪种选择是最优的。
例如矩阵连乘问题,我们假设已经知道在第k个矩阵加括号是最优的,即(A i A i+1…A k)(A k+1A k+2…A j)。
- 最优选择后会产生哪些子问题。
例如矩阵连乘问题,我们作出最优选择后产生两个子问题:(A i A i+1…A k),(A k+1A k+2…A j)。
- 证明原问题的最优解包含其子问题的最优解。
通常使用“剪切—粘贴”反证法。证明如果原问题的解是最优解,那么子问题的解也是最优解。反证:假定子问题的解不是最优解,那么就可以将它“剪切”掉,把最优解“粘贴”进去,从而得到一个比原问题最优解更优的解,这与前提原问题的解是最优解矛盾。得证。
例如:矩阵连乘问题,c=a+b+d,我们只需要证明如果c是最优的,则a和b一定是最优的(即原问题的最优解包含子问题的最优解)。
反证法: 如果a不是最优的,(A i A i+1…A k)存在一个最优解a’,a’<a,那么,a’+b+d<c,这与假设c是最优的矛盾,因此如果c是最优的,则a一定是最优的。同理可证b也是最优的。因此如果c是最优的,则a和b一定是最优的。因此,矩阵连乘问题具有最优子结构性质。
(2)如何得到最优解递归式
- 分析原问题最优解和子问题最优解的关系。
例如矩阵连乘问题,我们假设已经知道在第k个矩阵加括号是最优的,即(A i A i+1…A k) (A k+1A k+2…A j)。作出最优选择后产生两个子问题:(A i A i+1…A k),(A k+1A k+2…A j)。如果我们用m[i][j]表示A i A i+1…A j矩阵连乘的最优解,那么两个子问题(A i A i+1…A k)、(A k+1A k+2…A j)对应的最优解分别是m[i][k]、m[k+1][j]。剩下的只需要考查(A i A i+1…A k)和(A k+1A k+2…A j)的结果矩阵相乘的乘法次数了,两个结果矩阵相乘的乘法次数是pi*pk+1*qj。
因此,原问题最优解和子问题最优解的关系为m[i][j]=m[i][k]+m[k+1][j]+ pi*pk+1*qj。
- 考查有多少种选择。
实质上,我们并不知道哪种选择是最优的,因此就需要考查有多少种选择,然后从这些选择中找到最优解。
例如矩阵连乘问题,加括号的位置k(A i A i+1…A k)(A k+1A k+2…A j),k的取值范围是{i,i+1,…,j−1},即i≤k<j,那么我们考查每一种选择,找到最优值。
- 得到最优解递归式。
例如矩阵连乘问题,m[i][j]表示A i A i+1…A j矩阵连乘的最优解,根据最优解和子问题最优解的关系,并考查所有的选择,找到最小值即为最优解。