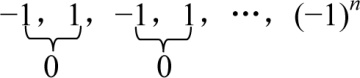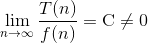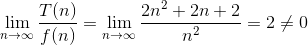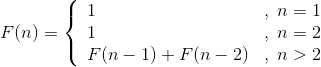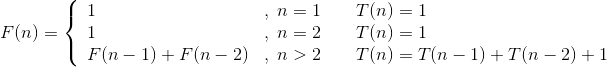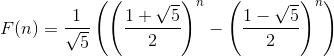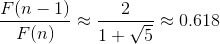《趣学算法》——第一章(算法之美)
第一章 算法之美
如果说数学是皇冠上的一颗明珠,那么算法就是这颗明珠上的光芒,算法让这颗明珠更加熠熠生辉,为科技进步和社会发展照亮了前进的路。数学是美学,算法是艺术。走进算法的人,才能体会它的魅力。
多年来,我有一个梦想,希望每一位提到算法的人,不再立即紧皱眉头,脑海闪现枯燥的公式、冗长的代码;希望每一位阅读和使用算法的人,体会到算法之美,像躺在法国普罗旺斯小镇的长椅上,呷一口红酒,闭上眼睛,体会舌尖上的美味,感受鼻腔中满溢的薰衣草的芳香……
1.1 打开算法之门
瑞士著名的科学家N.Wirth教授曾提出: 数据结构+算法=程序 。
数据结构是程序的骨架,算法是程序的灵魂。
在我们的生活中,算法无处不在。我们每天早上起来,刷牙、洗脸、吃早餐,都在算着时间,以免上班或上课迟到;去超市购物,在资金有限的情况下,考虑先买什么、后买什么,算算是否超额;在家中做饭,用什么食材、调料,做法、步骤,还要品尝一下咸淡,看看是否做熟。所以,不要说你不懂算法,其实你每天都在用!
但是对计算机专业算法,很多人都有困惑:“I can understand, but I can’tuse!”,我能看懂,但不会用!就像参观莫高窟的壁画,看到它、感受它,却无法走进。我们正需要一把打开算法之门的钥匙,就如陶渊明《桃花源记》中的“初极狭,才通人。复行数十步,豁然开朗。”
1.2 妙不可言——算法复杂性
我们首先看一道某跨国公司的招聘试题。
写一个算法,求下面序列之和:
−1,1,−1,1,…,(−1)n
当你看到这个题目时,你会怎么想?for语句?while循环?
先看算法1-1:
1 | //算法1-1 |
这段代码可以实现求和运算,但是为什么不这样算?!
再看算法1-2:
1 | //算法1-2 |
有的人看到这个代码后恍然大悟,原来可以这样啊?这不就是数学家高斯使用的算法吗?
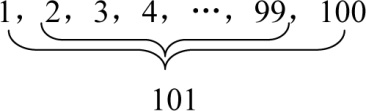
一共50对数,每对之和均为101,那么总和为:
(1+100)×50=5050
1787年,10岁的高斯用了很短的时间算出了结果,而其他孩子却要算很长时间。
可以看出,算法1-1需要运行n+1次,如果n=100 00,就要运行100 01次,而算法1-2仅仅需要运行1次!是不是有很大差别?
高斯的方法我也知道,但遇到类似的题还是……我用的笨办法也是算法吗?
答:是算法。
算法是指对特定问题求解步骤的一种描述。
算法只是对问题求解方法的一种描述,它不依赖于任何一种语言,既可以用自然语言、程序设计语言(C、C++、Java、Python等)描述,也可以用流程图、框图来表示。一般为了更清楚地说明算法的本质,我们去除了计算机语言的语法规则和细节,采用“伪代码”来描述算法。“伪代码”介于自然语言和程序设计语言之间,它更符合人们的表达方式,容易理解,但不是严格的程序设计语言,如果要上机调试,需要转换成标准的计算机程序设计语言才能运行。
算法具有以下特性。
(1) 有穷性 :算法是由若干条指令组成的有穷序列,总是在执行若干次后结束,不可能永不停止。
(2) 确定性 :每条语句有确定的含义,无歧义。
(3) 可行性 :算法在当前环境条件下可以通过有限次运算实现。
(4) 输入输出 :有零个或多个输入,一个或多个输出。
算法1-2的确算得挺快的,但如何知道我写的算法好不好呢?
“好”算法的标准如下。
(1)正确性:正确性是指算法能够满足具体问题的需求,程序运行正常,无语法错误,能够通过典型的软件测试,达到预期的需求。
(2)易读性:算法遵循标识符命名规则,简洁易懂,注释语句恰当适量,方便自己和他人阅读,便于后期调试和修改。
(3)健壮性:算法对非法数据及操作有较好的反应和处理。例如,在学生信息管理系统中登记学生年龄时,若将21岁误输入为210岁,系统应该提示出错。
(4)高效性:高效性是指算法运行效率高,即算法运行所消耗的时间短。算法时间复杂度就是算法运行需要的时间。现代计算机一秒钟能计算数亿次,因此不能用秒来具体计算算法消耗的时间,由于相同配置的计算机进行一次基本运算的时间是一定的,我们可以用算法基本运算的执行次数来衡量算法的效率。因此,将算法基本运算的执行次数作为时间复杂度的衡量标准。
(5)低存储性:低存储性是指算法所需要的存储空间低。对于像手机、平板电脑这样的嵌入式设备,算法如果占用空间过大,则无法运行。算法占用的空间大小称为 空间复杂度 。
除了(1)~(3)中的基本标准外,我们对好的算法的评判标准就是 高效率 、 低存储 。
(1)~(3)中的标准都好办,但时间复杂度怎么算呢?
时间复杂度 :算法运行需要的时间,一般将 算法的执行次数 作为时间复杂度的度量标准。
看算法1-3,并分析算法的时间复杂度。
1 | //算法1-3 |
把算法的所有语句的运行次数加起来:1+1+n+n+n×n+n×n,可以用一个函数T(n)表达:
T(n)=2n2+2n+2
当n足够大时,例如n=105时,T(n)=2×1010+2×105+2,我们可以看到算法运行时间主要取决于第一项,后面的甚至可以忽略不计。
用极限表示为:
,C为不等于0的常数
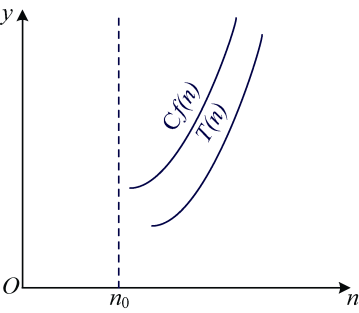
如果用 时间复杂度的渐近上界 表示,如图1-1所示。
从图1-1中可以看出,当n≥n0时,T(n)≤Cf (n),当n足够大时,T(n)和f (n)近似相等。因此,我们用О(f (n))来表示时间复杂度渐近上界,通常用这种表示法衡量算法时间复杂度。算法1-3的时间复杂度渐近上界为О(f (n))=О(n2),用极限表示为:
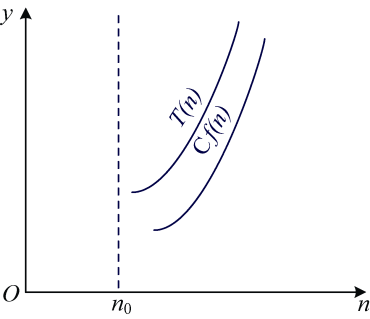
还有 渐近下界 符号Ω(T(n)≥Cf (n)),如图1-2所示。
从图1-2可以看出,当n≥n0时,T(n)≥Cf (n),当n足够大时,T(n)和f (n)近似相等,因此,我们用Ω(f (n))来表示时间复杂度渐近下界。
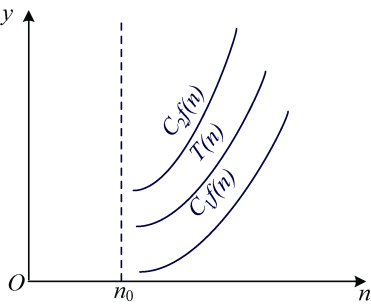
渐近精确界 符号Θ(C1f (n)≤T(n)≤C2f (n)),如图1-3所示。
从图1-3中可以看出,当n≥n0时,C1f (n)≤T(n)≤C2f (n),当n足够大时,T(n)和f (n)近似相等。这种两边逼近的方式,更加精确近似,因此,用Θ (f (n))来表示时间复杂度渐近精确界。
我们通常使用时间复杂度渐近上界О(f (n))来表示时间复杂度。
看算法1-4,并分析算法的时间复杂度。
1 | //算法1-4 |
观察算法1-4,无法立即确定while 及i=i*2运行了多少次。这时可假设运行了x次,每次运算后i值为2,22,23,…,2x,当i=n时结束,即2x=n时结束,则x=log2n,那么算法1-4的运算次数为1+2log2n,时间复杂度渐近上界为О(f (n))=О(log2n)。
在算法分析中,渐近复杂度是对算法运行次数的粗略估计,大致反映问题规模增长趋势,而不必精确计算算法的运行时间。在计算渐近时间复杂度时,可以只考虑对算法运行时间贡献大的语句,而忽略那些运算次数少的语句,循环语句中处在循环内层的语句往往运行次数最多,即为对运行时间贡献最大的语句。例如在算法1-3中,total=total+i*j是对算法贡献最大的语句,只计算该语句的运行次数即可。
注意: 不是每个算法都能直接计算运行次数。
例如算法1-5,在a[n]数组中顺序查找x,返回其下标i,如果没找到,则返回−1。
1 | //算法1-5 |
我们很难计算算法1-5中的程序到底执行了多少次,因为运行次数依赖于x在数组中的位置,如果第一个元素就是x,则执行1次(最好情况);如果最后一个元素是x,则执行n次(最坏情况);如果分布概率均等,则平均执行次数为(n+1)/2。
有些算法,如排序、查找、插入等算法,可以分为 最好 、 最坏 和 平均 情况分别求算法渐近复杂度,但我们考查一个算法通常考查最坏的情况,而不是考查最好的情况, 最坏情况对衡量算法的好坏具有实际的意义 。
我明白了,那空间复杂度应该就是算法占了多大存储空间了?
空间复杂度 :算法占用的空间大小。一般将算法的 辅助空间 作为衡量空间复杂度的标准。
空间复杂度的本意是指算法在运行过程中占用了多少存储空间。算法占用的存储空间包括:
(1)输入/输出数据;
(2)算法本身;
(3)额外需要的辅助空间。
输入/输出数据占用的空间是必需的,算法本身占用的空间可以通过精简算法来缩减,但这个压缩的量是很小的,可以忽略不计。而在运行时使用的辅助变量所占用的空间,即辅助空间是衡量空间复杂度的关键因素。
看算法1-6,将两个数交换,并分析其空间复杂度。
1 | //算法1-6 |
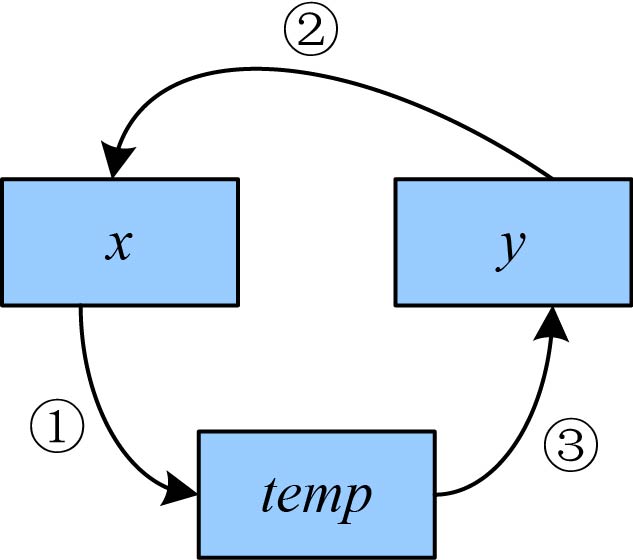
两数的交换过程如图1-4所示。
图1-4中的步骤标号与算法1-6中的语句标号一一对应,该算法使用了一个辅助空间temp,空间复杂度为О(1)。
注意: 递归算法中,每一次递推需要一个栈空间来保存调用记录,因此,空间复杂度需要计算递归栈的辅助空间。
看算法1-7,计算n的阶乘,并分析其空间复杂度。
1 | //算法1-7 |
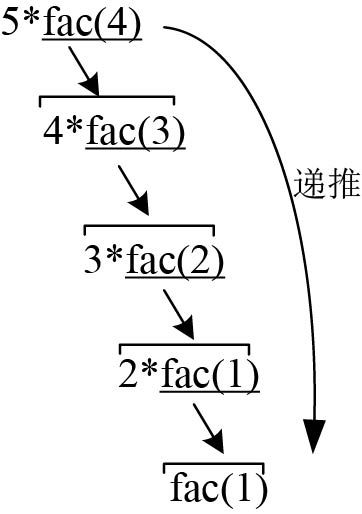
阶乘是典型的递归调用问题,递归包括递推和回归。递推是将原问题不断分解成子问题,直到达到结束条件,返回最近子问题的解;然后逆向逐一回归,最终到达递推开始的原问题,返回原问题的解。
思考: 试求5的阶乘,程序将怎样计算呢?
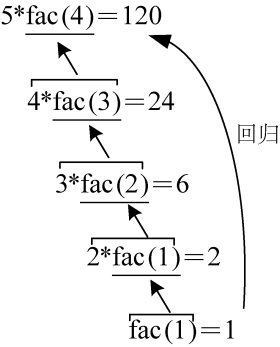
5的阶乘的递推和回归过程如图1-5和图1-6所示。
图1-5和图1-6的递推、回归过程是我们从逻辑思维上推理,用图的方式形象地表达出来的,但计算机内部是怎样处理的呢?计算机使用一种称为“栈”的数据结构,它类似于一个放一摞盘子的容器,每次从顶端放进去一个,拿出来的时候只能从顶端拿一个,不允许从中间插入或抽取,因此称为“后进先出”(last in first out)。
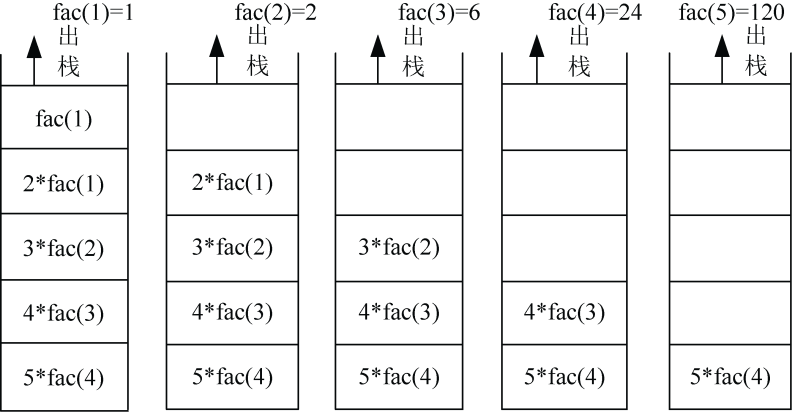
5的阶乘进栈过程如图1-7所示。
5的阶乘出栈过程如图1-8所示。
从图1-7和图1-8的进栈、出栈过程中,我们可以很清晰地看到,首先把子问题一步步地压进栈,直到得到返回值,再一步步地出栈,最终得到递归结果。在运算过程中,使用了n个栈空间作为辅助空间,因此阶乘递归算法的空间复杂度为О(n)。在算法1-7中,时间复杂度也为О(n),因为n的阶乘仅比n−1的阶乘多了一次乘法运算,fac(n)=n*fac(n−1)。如果用T(n)表示fac(n)的时间复杂度,可表示为:
T(n)= T(n−1)+1
= T(n−2)+1+1
……
= T(1)+…+1+1
=n
1.3 美不胜收——魔鬼序列
趣味故事1-1:一棋盘的麦子
有一个古老的传说,有一位国王的女儿不幸落水,水中有很多鳄鱼,国王情急之下下令:“谁能把公主救上来,就把女儿嫁给他。”很多人纷纷退让,一个勇敢的小伙子挺身而出,冒着生命危险把公主救了上来,国王一看是个穷小子,想要反悔,说:“除了女儿,你要什么都可以。”小伙子说:“好吧,我只要一棋盘的麦子。您在第1个格子里放1粒麦子,在第2个格子里放2粒,在第3个格子里放4粒,在第4个格子里放8粒,以此类推,每一格子里的麦子粒数都是前一格的两倍。把这64个格子都放好了就行,我就要这么多。”国王听后哈哈大笑,觉得小伙子的要求很容易满足,满口答应。结果发现,把全国的麦子都拿来,也填不完这64格……国王无奈,只好把女儿嫁给了这个小伙子。
解析
棋盘上的64个格子究竟要放多少粒麦子?
把每一个放的麦子数加起来,总和为S,则:
S=1+21+22+23+…+263 ①
我们把式①等号两边都乘以2,等式仍然成立:
2S=21+22+23+…+263+264 ②
式 ②减去式①,则:
S=264−1 =18 446 744 073 709 551 615
据专家统计,每个麦粒的平均重量约41.9毫克,那么这些麦粒的总重量是:
18 446 744 073 709 551 615×41.9=772 918 576 688 430 212 668.5(毫克)
≈7729(亿吨)
全世界人口按60亿计算,每人可以分得128吨!
我们称这样的函数为 爆炸增量函数 ,想一想,如果算法时间复杂度是О(2n) 会怎样?随着n的增长,这个算法会不会“爆掉”?经常见到有些算法调试没问题,运行一段也没问题,但关键的时候宕机(shutdown)。例如,在线考试系统,50个人考试没问题,100人考试也没问题,如果全校1万人考试就可能出现宕机。
注意: 宕机就是死机,指电脑不能正常工作了,包括一切原因导致的死机。计算机主机出现意外故障而死机,一些服务器(如数据库)死锁,服务器的某些服务停止运行都可以称为宕机。
常见的算法时间复杂度有以下几类。
(1)常数阶。
常数阶算法运行的次数是一个常数,如5、20、100。常数阶算法时间复杂度通常用О(1)表示,例如算法1-6,它的运行次数为4,就是常数阶,用О(1)表示。
(2)多项式阶。
很多算法时间复杂度是多项式,通常用О(n)、О(n2)、О(n3)等表示。例如算法1-3就是多项式阶。
(3)指数阶。
指数阶时间复杂度运行效率极差,程序员往往像躲“恶魔”一样避开它。常见的有О(2n)、О(n!)、О(nn)等。使用这样的算法要慎重,例如趣味故事1-1。
(4)对数阶。
对数阶时间复杂度运行效率较高,常见的有О(logn)、О(nlogn)等,例如算法1-4。
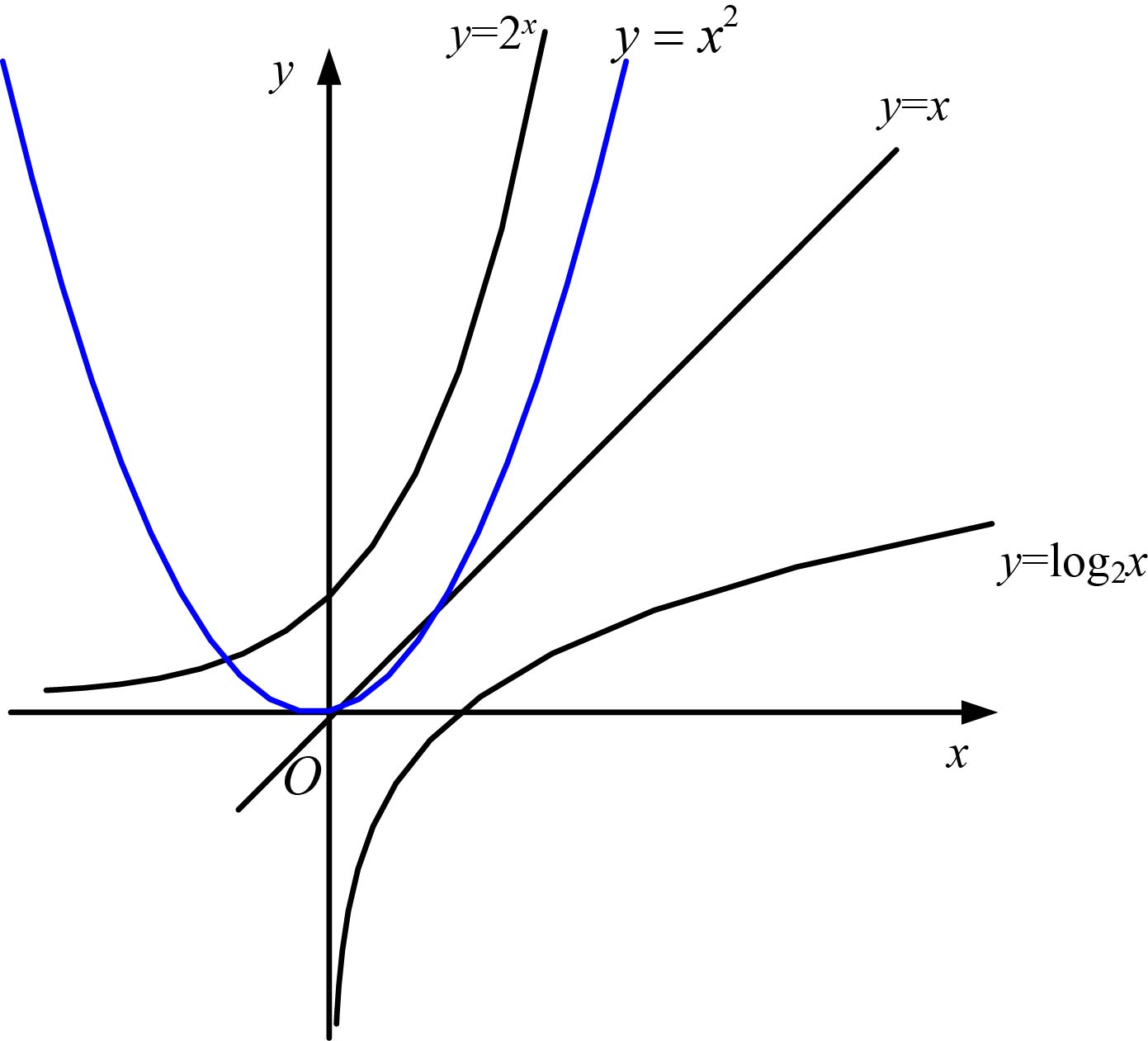
常见时间复杂度函数曲线如图1-9所示。
从图1-9中可以看出,指数阶增量随着x的增加而急剧增加,而对数阶增加缓慢。它们之间的关系为:
О(1)< О(logn)< О(n)< О(nlogn) < О(n2)< О(n3)< О(2n) < О(n!)< О(nn)
我们在设计算法时要注意算法复杂度增量的问题,尽量避免爆炸级增量。
趣味故事1-2:神奇兔子数列
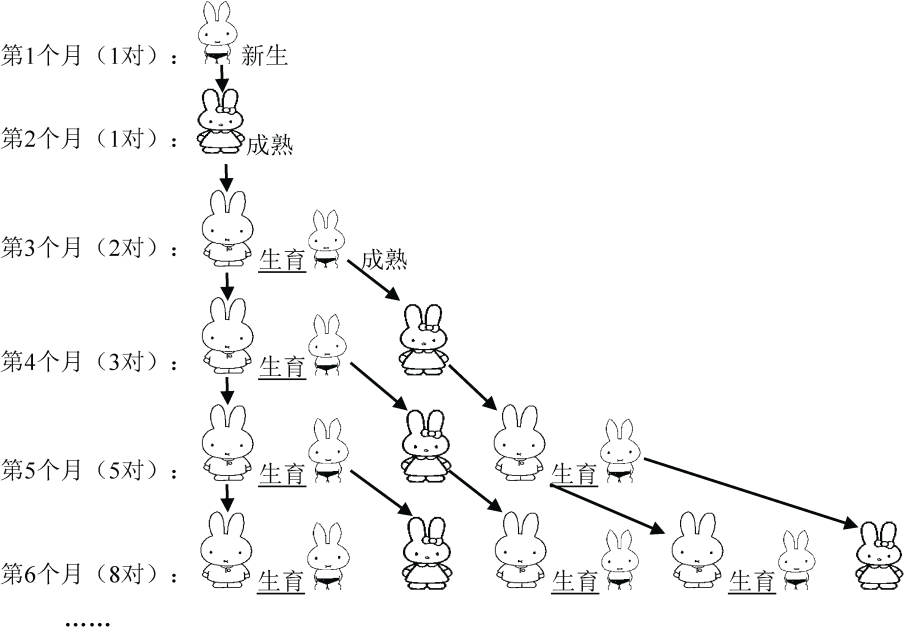
假设第1个月有1对刚诞生的兔子,第2个月进入成熟期,第3个月开始生育兔子,而1对成熟的兔子每月会生1对兔子,兔子永不死去……那么,由1对初生兔子开始,12个月后会有多少对兔子呢?
兔子数列即斐波那契数列,它的发明者是意大利数学家列昂纳多•斐波那契(Leonardo Fibonacci,1170—1250)。1202年,他撰写了《算盘全书》(《Liber Abaci》)一书,该书是一部较全面的初等数学著作。书中系统地介绍了印度—阿拉伯数码及其演算法则,介绍了中国的“盈不足术”;引入了负数,并研究了一些简单的一次同余式组。
(1)问题分析
我们不妨拿新出生的1对小兔子分析:
第1个月,小兔子①没有繁殖能力,所以还是1对。
第2个月,小兔子①进入成熟期,仍然是1对。
第3个月,兔子①生了1对小兔子②,于是这个月共有2(1+1=2)对兔子。
第4个月,兔子①又生了1对小兔子③。因此共有3(1+2=3)对兔子。
第5个月,兔子①又生了1对小兔子④,而在第3个月出生的兔子②也生下了1对小兔子⑤。共有5(2+3=5)对兔子。
第6个月,兔子①②③各生下了1对小兔子。新生3对兔子加上原有的5对兔子这个月共有8(3+5=8)对兔子。
……
为了表达得更清楚,我们用图示来分别表示新生兔子、成熟期兔子和生育期兔子,兔子的繁殖过程如图1-10所示。
这个数列有十分明显的特点,从第3个月开始, 当月的兔子数 = 上月兔子数 + 当月新生兔子数 ,而当月新生的兔子正好是 上上月的兔子数 。因此,前面相邻两项之和,构成了后一项,即:
当月的兔子数 = 上月兔子数 + 上上月的兔子数
斐波那契数列如下:
1,1,2,3,5,8,13,21,34,…
递归式表达式:
那么我们该怎么设计算法呢?
哈哈,这太简单了,用递归算法很快就算出来了!
(2)算法设计
首先按照递归表达式设计一个递归算法,见算法1-8。
1 | //算法1-8 |
写得不错,那么算法设计完成后,我们有3个问题:
- 算法是否正确?
- 算法复杂度如何?
- 能否改进算法?
(3)算法验证分析
第一个问题毋庸置疑,因为算法1-8是完全按照递推公式写出来的,所以正确性没有问题。那么算法复杂度呢?假设T(n)表示计算Fib1(n)所需要的基本操作次数,那么:
1 | n=1时,T(n)=1; |
因此,n>2时要分别调用Fib1(n−1)、Fib1(n−2)和执行一次加法运算,即:
1 | n>2时,T(n)= T(n-1)+ T(n-2)+1; |
递归表达式和时间复杂度T(n)之间的关系如下:
由此可得:。
那么怎么计算F(n)呢?
有兴趣的读者可以看本书附录A中通项公式的求解方法,也可以看下文中的简略解释。
斐波那契数列通项为:
当n趋近于无穷时,
由于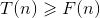
如果我们今年计算出了F(100),那么明年才能算出F(101),多算一个斐波那契数需要一年的时间, 爆炸增量函数 是算法设计的噩梦!算法1-8的时间复杂度属于 爆炸增量函数 ,这在算法设计时是应当避开的,那么我们能不能改进它呢?
(4)算法改进
既然斐波那契数列中的每一项是前两项之和,如果记录前两项的值,只需要一次加法运算就可以得到当前项,时间复杂度会不会更低一些?我们用数组试试看,见算法1-9。
1 | //算法1-9 |
很明显,算法1-9的时间复杂度为О(n)。算法仍然是按照F(n)的定义,所以正确性没有问题,而 时间复杂度 却从算法1-8的 指数阶降到了多项式阶 ,这是算法效率的一个巨大突破!
算法1-9使用了一个辅助数组记录中间结果,空间复杂度也为О(n),其实我们只需要得到第n个斐波那契数,中间结果只是为了下一次使用,根本不需要记录。因此,我们可以采用 迭代法 进行算法设计,见算法1-10。
1 | //算法1-10 |
迭代过程如下。
初始值:s1=1;s2=1;
当前解 记录前一项
i=3时 s2= s1+s2=2 s1=s2−s1=1
i=4时 s2= s1+s2=3 s1= s2−s1=2
i=5时 s2= s1+s2=5 s1= s2−s1=3
i=6时 s2= s1+s2=8 s1= s2−s1=5
…… …… ……
算法1-10使用了若干个辅助变量,迭代辗转相加,每次记录前一项,时间复杂度为О(n),但 空间复杂度 降到了О(1)。
问题的进一步讨论 :我们能不能继续降阶,使算法时间复杂度更低呢?实质上,斐波那契数列时间复杂度还可以降到对数阶О(logn),有兴趣的读者可以查阅相关资料。想想看,我们把一个算法从 指数阶 降到 多项式阶 ,再降到 对数阶 ,这是一件多么振奋人心的事!
(5)惊人大发现
科学家经研究在植物的叶、枝、茎等排列中发现了斐波那契数!例如,在树木的枝干上选一片叶子,记其为数1,然后依序点数叶子(假定没有折损),直到到达与那片叶子正对的位置,则其间的叶子数多半是斐波那契数。叶子从一个位置到达下一个正对的位置称为一个循回。叶子在一个循回中旋转的圈数也是斐波那契数。在一个循回中,叶子数与叶子旋转圈数的比称为叶序(源自希腊词,意即叶子的排列)比。多数植物的叶序比呈现为斐波那契数的比,例如,蓟的头部具有13条顺时针旋转和21条逆时针旋转的斐波那契螺旋,向日葵的种子的圈数与子数、菠萝的外部排列同样有着这样的特性,如图1-11所示。
观察延龄草、野玫瑰、南美血根草、大波斯菊、金凤花、耧斗菜、百合花、蝴蝶花的花瓣,可以发现它们的花瓣数目为斐波那契数:3,5,8,13,21,…。如图1-12所示。
树木在生长过程中往往需要一段“休息”时间,供自身生长,而后才能萌发新枝。所以,一株树苗在一段间隔(例如一年)以后长出一条新枝;第二年新枝“休息”,老枝依旧萌发;此后,老枝与“休息”过一年的枝同时萌发,当年生的新枝则次年“休息”。这样,一株树木各个年份的枝桠数便构成斐波那契数列,这个规律就是生物学上著名的“鲁德维格定律”。
这些植物懂得斐波那契数列吗?应该并非如此,它们只是按照自然的规律才进化成这样的。这似乎是植物排列种子的“优化方式”,它能使所有种子具有相近的大小却又疏密得当,不至于在圆心处挤太多的种子而在圆周处却又很稀疏。叶子的生长方式也是如此,对于许多植物来说,每片叶子从中轴附近生长出来,为了在生长的过程中一直都能最佳地利用空间(要考虑到叶子是一片一片逐渐地生长出来,而不是一下子同时出现的),每片叶子和前一片叶子之间的角度应该是222.5°,这个角度称为“黄金角度”,因为它和整个圆周360°之比是黄金分割数0.618的倒数,而这种生长方式就导致了斐波那契螺旋的产生。向日葵的种子排列形成的斐波那契螺旋有时能达到89,甚至144。1992年,两位法国科学家通过对花瓣形成过程的计算机仿真实验,证实了在系统保持最低能量的状态下,花朵会以斐波那契数列的规律长出花瓣。
有趣的是:这样一个完全是自然数的数列,通项公式却是用无理数来表达的。而且当n趋向于无穷大时,斐波那契数列前一项与后一项的比值越来越逼近黄金分割比0.618:1÷1 = 1,1÷2 = 0.5,2÷3 = 0.666,…,3÷5 = 0.6,5÷8 = 0.625,…,55÷89 = 0.617977,…,144÷233 = 0.618025,…,46368÷75025 = 0.6180339886……
越到后面,这些比值越接近黄金分割比:
斐波那契数列起源于兔子数列,这个现实中的例子让我们真切地感到数学源于生活,生活中我们需要不断地通过现象发现数学问题,而不是为了学习而学习。学习的目的是满足对世界的好奇心,如果我们怀着这样一颗好奇心,或许世界会因你而不同!斐波那契通过兔子繁殖来告诉我们这种数学问题的本质,随着数列项的增加,前一项与后一项之比越来越逼近黄金分割的数值0.618时,我彻底被震惊到了,因为数学可以表达美,这是令我们叹为观止的地方。当数学创造了更多的奇迹时,我们会发现数学本质上是可以回归到自然的,这样的事例让我们感受到数学的美,就像黄金分割、斐波那契数列,如同大自然中的一朵朵小花,散发着智慧的芳香……
1.4 灵魂之交——马克思手稿中的数学题
有人抱怨:算法太枯燥、乏味了,看到公式就头晕,无法学下去了。你肯定选择了一条充满荆棘的路。选对方法,你会发现这里是一条充满鸟语花香和欢声笑语的幽径,在这里,你可以和高德纳聊聊,同爱因斯坦喝杯咖啡,与歌德巴赫和角谷谈谈想法,Dijkstra也不错。与世界顶级的大师进行灵魂之交,不问结果,这一过程已足够美妙!
如果这本书能让多一个人爱上算法,这就足够了!
趣味故事1-3:马克思手稿中的数学题
马克思手稿中有一道趣味数学问题:有30个人,其中有男人、女人和小孩,这些人在一家饭馆吃饭花了50先令;每个男人花3先令,每个女人花2先令,每个小孩花1先令;问男人、女人和小孩各有几人?
(1)问题分析
设x、y、z分别代表男人、女人和小孩。按题目的要求,可得到下面的方程:
x+y+z=30 ①
3x+2y+z=50 ②
两式相减,②−①得:
2x+y=20 ③
从式③可以看出,因为x、y为正整数,x最大只能取9,所以x变化范围是1~9。那么我们可以让x从1到9变化,再找满足①②两个条件y、z值,找到后输入即可,答案可能不止一个。
(2)算法设计
按照上面的分析进行算法设计,见算法1-11。
1 | //算法1-11 |
(3)算法分析
算法完全按照题中方程设计,因此正确性毋庸置疑。那么算法复杂度怎样呢?从算法1-11中可以看出,对算法时间复杂度贡献最大的语句是for(x=1;x<=9;x++),该语句的执行次数是9,for循环中3条语句的执行次数也为9,其他语句执行次数为1,for语句一共执行36次基本运算,时间复杂度为О(1)。没有使用辅助空间,空间复杂度也为О(1)。
(4)问题的进一步讨论
为什么让x变化来确定y、z值?让y变化来确定x、z值会怎样呢?让z变化来确定x、y值行不行?有没有更好的算法降低时间复杂度?
趣味故事1-4:爱因斯坦的阶梯
爱因斯坦家里有一条长阶梯,若每步跨2阶,则最后剩1阶;若每步跨3阶,则最后剩2阶;若每步跨5阶,则最后剩4阶;若每步跨6阶,则最后剩5阶。只有每次跨7阶,最后才正好1阶不剩。请问这条阶梯共有多少阶?
(1)问题分析
根据题意,阶梯数n满足下面一组同余式:
n≡1(mod2)
n≡2(mod3)
n≡4(mod5)
n≡5(mod6)
n≡0(mod7)
注意: 两个整数a、b,若它们除以整数m所得的余数相等,则称a、b对于模m同余,记作a≡b(mod m),读作a同余于b模m,或读作a与b关于模m同余。那么只需要判断一个整数值是否满足这5个同余式即可。
(2)算法设计
按照上面的分析进行算法设计,见算法1-12。
1 | //算法1-12 |
(3)算法分析
算法的运行结果:
1 | Count the stairs =119 |
因为n从1开始,找到第一个满足条件的数就停止,所以算法1-12中的while语句运行了119次。有的算法从算法本身无法看出算法的运行次数,例如算法1-12,我们很难知道while语句执行了多少次,因为它是满足条件时停止,那么多少次才能满足条件呢?每个问题具体的次数是不同的,所以不能看到程序中有n,就简单地说它的时间复杂度为n。
我们从1开始一个一个找结果的办法是不是太麻烦了?
(4)算法改进
因为从上面的5个同余式来看,这个数一定是7的倍数n≡0(mod 7),除以6余5,除以5余4,除以3余2,除以2余1,我们为什么不从7的倍数开始判断呢?算法改进见算法1-13。
1 | //算法1-13 |
算法的运行结果:
1 | Count the stairs =119 |
算法1-13中的while语句执行了119/7=17次,可见运行次数减少了不少呢!
(5)问题的进一步讨论
此题算法还可考虑求1、2、4、5的最小公倍数n,然后令t=n−1,判断t≡0(mod 7)是否成立,若不成立则t=t+n,再进行判别,直到选出满足条件的t为止。
1、2、4、5的最小公倍数n=20。
t=n-1=19,t≡0(mod 7)不成立;
t= t+n=39,t≡0(mod 7)不成立;
t= t+n=59,t≡0(mod 7)不成立;
t= t+n=79,t≡0(mod 7)不成立;
t= t+n=99,t≡0(mod 7)不成立;
t= t+n=119,t≡0(mod 7)成立。
我们可以看到这一算法判断6次即成功,但是,求多个数的最小公倍数需要多少时间复杂度,是不是比上面的算法更优呢?结果如何请大家动手试一试。
趣味故事1-5:哥德巴赫猜想
哥德巴赫猜想:任一大于2的偶数,都可表示成两个素数之和。
验证:2000以内大于2的偶数都能够分解为两个素数之和。
(1)问题分析
为了验证哥德巴赫猜想对2000以内大于2的偶数都是成立的,要将整数分解为两部分(两个整数之和),然后判断分解出的两个整数是否均为素数。若是,则满足题意;否则重新进行分解和判断。素数测试的算法可采用试除法,即用2,3,4,…,
(2)算法设计
按照上面的分析进行算法设计,见算法1-14。
1 | //算法1-14 |
(3)算法分析
要验证哥德巴赫猜想对2000以内大于2的偶数都是成立的,我们首先要看看这个范围的偶数有多少个。1~2000中有1000个偶数,1000个奇数,那么大于2的偶数有999个,即i=4,6,8,…,2000。再看偶数分解和素数判断,这就要看最好情况和最坏情况了。最好的情况是一次分解,两次素数判断即可成功,最坏的情况要i−2次分解(即n=2,3,…,i−1的情况),每次分解分别执行2~sqrt(n)次、2~sqrt(i−n)次判断。
这个程序看似简单合理,但存在下面两个问题。
1)偶数分解存在重复。
- i=4:分解为(2,2),(3,1),从n=2,3,…,i−1分解,每次得到一组数(n,i−n)。
- i=6:分解为(2,4),(3,3),(4,2),(5,1)。
- i=8:分解为(2,6),(3,5),(4,4),(5,3),(6,2),(7,1)。
除了最后一项外,每组分解都在i/2处对称分布。最后一组中有一个数为1,1既不是素数也不是合数,因此去掉最后一组,那么我们就可以从n=2,3,…,i/2进行分解,省掉了一半的多余判断。
2)素数判断存在重复。
- i=4:分解为(2,2),(3,1),要判断2是否为素数,然后判断第二个2是否为素数。判断成功,返回。
- i=6:分解为(2,4),(3,3),(4,2),(5,1),要判断2是否为素数,然后判断4是否为素数,不是继续下一个分解。再判断3是否为素数,然后判断第二个3是否为素数。判断成功,返回。
每次判断素数都要调用prime函数,那么可以先判断分解有可能得到的数是否为素数,然后把结果存储下来,下次判断时只需要调用上次的结果,不需要再重新判断是否为素数。例如(2,2),第一次判断结果2是素数,那第二个2就不用判断,直接调用这个结果,后面所有的分解,只要遇到这个数就直接认定为这个结果。
(4)算法改进
先判断所有分解可能得到的数是否为素数,然后把结果存储下来,有以下两种方法。
1)用布尔型数组 flag[2…1998]记录分解可能得到的数(2~1998)所有数是不是素数,分解后的值作为下标,调用该数组即可。时间复杂度减少,但空间复杂度增加。
2)用数值型数组data[302]记录2~1998中所有的素数(302个)。
- 分解后的值,采用折半查找(素数数组为有序存储)的办法在素数数组中查找,找到就是素数,否则不是。
- 不分解,直接在素数数组中找两个素数之和是否为i,如果找到,验证成功。因为素数数组为有序存储,当两个数相加比i大时,不需要再判断后面的数。
(5)问题的进一步讨论
上面的方法可以写出3个算法,大家可以尝试写一写,然后分析时间复杂度、空间复杂度如何?哪个算法更优一些?是不是还可以做到更好?
1.5 算法学习瓶颈
很多人感叹:算法为什么这么难!
一个原因是,算法本身具有一定的复杂性,还有一个原因:讲得不到位!
算法的教与学有两个困难。
(1)我们学习了那些经典的算法,在惊叹它们奇妙的同时,难免疑虑重重:这些算法是怎么被想到的?这可能是最费解的地方。高手讲,学算法要学它的来龙去脉,包括种种证明。但这对菜鸟来说,这简直比登天还难,很可能花费很多时间也无法搞清楚。对大多数人来说,这条路是行不通的,那怎么办呢?下功夫去记忆书上的算法?记住这些算法的效率?这样做看似学会了,其实两手空空,遇到一个新问题,仍然无从下手。可这偏偏又是极重要的,无论做研究还是实际工作,一个计算机专业人士最重要的能力就是解决问题——解决那些不断从实际应用中冒出来的新问题。
(2)算法作为一门学问,有两条几乎平行的线索。一个是 数据结构 (数据对象):数、矩阵、集合、串、排列、图、表达式、分布等。另一个是 算法策略 :贪心、分治、动态规划、线性规划、搜索等。这两条线索是相互独立的:同一个数据对象(如图)上有不同的问题(如单源最短路径和多源最短路径),就可以用到不同的算法策略(例如贪婪和动态规划);而完全不同的数据对象上的问题(如排序和整数乘法),也许就会用到相同的算法策略(如分治)。
两条线索交织在一起,该如何表述?我们早已习惯在一章中完全讲排序,而在另一章中完全讲图论算法。还没有哪一本算法书很好地解决这两个困难,传统的算法书大多注重内容的收录,但却忽视思维过程的展示,因此我们学习了经典的算法,却费解于算法设计的过程。
本书从问题出发,根据实际问题分析、设计合适的算法策略,然后在数据结构上操作实现,巧妙地将数据结构和算法策略拧成了一条线。通过大量实例,充分展现算法设计的思维过程,让读者充分体会求解问题的思路,如何分析?使用什么算法策略?采用什么数据结构?算法的复杂性如何?是否有优化的可能?
这里,我们培养的是让读者怀着一颗好奇心去思考问题、解决问题。更重要的是——体会学习的乐趣,发现算法的美!
1.6 你怕什么
本章主要说明以下问题。
(1)将程序执行次数作为时间复杂度衡量标准。
(2)时间复杂度通常用渐近上界符号f(n)表示。
(3)衡量算法的好坏通常考查算法的最坏情况。
(4)空间复杂度只计算辅助空间。
(5)递归算法的空间复杂度要计算递归使用的栈空间。
(6)设计算法时尽量避免爆炸级增量复杂度。
通过本章的学习,我们对算法有了初步的认识,算法就在我们的生活中。任何一个算法都不是凭空造出来的,而是来源于实际中的某一个问题,由此推及一类、一系列问题,所以算法的本质是高效地解决实际问题。本章部分内容或许你不是很清楚,不必灰心,还记得我在前言中说的“ 大视野 , 不求甚解 ”吗?例如斐波那契数列的通项公式推导,不懂没关系,只要知道斐波那契数列用递归算法,时间复杂度是指数阶,这就够了。就像一个面包师一边和面,一边详细讲做好面包要多少面粉、多少酵母、多大火候,如果你对如何做面包非常好奇,大可津津有味地听下去,如果你只是饿了,那么只管吃好了。
通过算法,你可以与世界顶级大师进行灵魂交流,体会算法的妙处。
Donald Ervin Knuth说:“程序就是蓝色的诗”。而这首诗的灵魂就是算法,走进算法,你会发现无与伦比的美!
持之以恒地学习,没有什么是学不会的。行动起来,没有什么不可以!